Využití exaktních testů nejen ve zdravotnictví

V medicínských studiích se často vyskytují situace, kdy je nutné analyzovat malé soubory pacientů, kteří například trpí určitým vzácným onemocněním nebo podstupují nákladné vyšetření. V těchto případech však není možné pracovat běžnými statistickými postupy založenými na asymptotických metodách. Ty dobře fungují pouze tehdy, pokud jsou splněné určité předpoklady a je k dispozici dostatečný počet pozorování. Analýza malých datových souborů však vyžaduje, aby byla při testování hypotéz počítána dosažená hladina významnosti (signifikance) přesně. Podobný problém nastává i u větších souborů, pokud jsou například porovnávané skupiny velmi nerovnoměrně zastoupené. Program IBM SPSS Statistics pro tyto účely nabízí specializovaný modul Exact Tests.

Co jsou exaktní testy

Myšlenka exaktních testů vychází již z práce R. A. Fishera, možnosti jejich praktického využití však byly dlouho omezené z důvodu přílišné výpočetní náročnosti. Tyto postupy nacházejí své uplatnění tam, kde nejsou splněné předpoklady asymptotických metod, například v těchto situacích:

• malé datové soubory (více pozorování není k dispozici nebo by bylo by příliš nákladné je získat),
• zkoumání řídkých jevů i ve velkých datových souborech,
• vysoký počet malých skupin nebo velmi nerovnoměrně zastoupené skupiny.

Exaktní testy počítají přesnou pravděpodobnost stejně extrémního nebo extrémnějšího výsledku vzhledem k nulové hypotéze než je pozorovaný. Vycházejí při tom ze všech možných výsledků. Závěr je vždy věrohodný bez ohledu na velikost souboru nebo rozložení dat.

Výpočet exaktní pravděpodobnosti může být časově i výpočetně velmi náročný a někdy může i překročit kapacity paměti počítače. Pro jednotlivé typy testů existují různá doporučení ohledně velikosti souboru, obecně však lze říci, že výpočet by měl proběhnout rychle, pokud počet případů nepřesáhne třicet. Zároveň lze pro výpočet také nastavit časový limit.

Pokud je třeba pracovat exaktními metodami, ale výpočet by trval příliš dlouho, je možné odhadnout exaktní pravděpodobnost s požadovanou přesností pomocí metody Monte Carlo. Ta je výpočetně méně náročná, protože nepracuje se všemi možnými výsledky, ale pouze s náhodným výběrem z nich (i zde se však řádově jedná o desítky tisíc takto generovaných výběrů). Pro větší soubory poskytuje metoda Monte Carlo nevychýlený odhad exaktní signifikance včetně intervalu spolehlivosti bez nutnosti pracovat s asymptotickými metodami.

Program IBM SPSS Statistics počítá standardně v základním modulu Base dosažené hladiny významnosti v procedurách Crosstabs a Nonparametric Tests asymptotickým způsobem. Výsledek je založen na předpokladu určitého rozložení testové statistiky při dostatečně velkém počtu případů. Modul Exact Tests rozšiřuje tyto procedury o možnost výpočtu exaktní dosažené hladiny významnosti nebo jejího odhadu metodou Monte Carlo. Celkem se jedná o více než třicet neparametrických testů nebo testů určených pro analýzu kategorizovaných dat v kontingenční tabulce. Interpretace výsledků je stejná jako u jakýchkoliv jiných testů v IBM SPSS Statistics Base, pro jejich výpočet se však užívá jiný statistický algoritmus.

Příklad

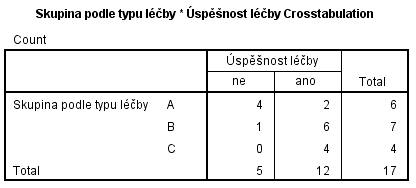
Užití exaktního testu si ukážeme na následujícím příkladu. V rámci pilotní studie se porovnávala úspěšnost léčby ve třech skupinách pacientů podle typu léčby. Do výzkumu bylo celkem zapojeno 17 pacientů, Tabulka 1 shrnuje úspěšnost v jednotlivých skupinách. Cílem následující analýzy je otestovat, zda existuje vztah mezi typem léčby a její úspěšností.

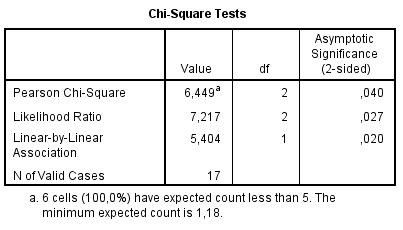
Tabulka 2 zobrazuje na prvním řádku výsledek asymptotického Pearsonova testu chí-kvadrát. Dosažená hladina významnosti je 0,04, na základě tohoto testu bychom tedy na 95% hladině spolehlivosti zamítli nulovou hypotézu nezávislosti. Poznámka pod tabulkou ale upozorňuje, že ve všech polích tabulky je očekávaná četnost menší než 5. Pro užití tohoto testu se však doporučuje, aby takových polí bylo maximálně 20 %. Předpoklady asymptotického testu tedy nejsou splněné, proto dosaženou hladinu významnosti raději spočítáme exaktním způsobem.

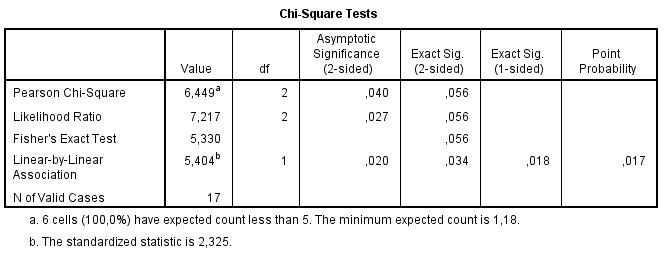
Při sedmnácti případech proběhl výpočet exaktní dosažené hladiny významnosti téměř okamžitě a tabulka se rozšířila o další tři sloupce (viz Tabulka 3). Pro naši úlohu je podstatná především hodnota exaktní dosažené hladiny významnosti při oboustranné alternativní hypotéze Pearsonova testu chí-kvadrát (Exact Sig. (2-sided)). Vzhledem k tomu, že hodnota 0,056 je větší než 5%, nezamítáme na 95% hladině spolehlivosti nulovou hypotézu nezávislosti. V tomto případě tedy přesný výpočet dosažené hladiny významnosti vede k odlišnému závěru než asymptotický – vztah mezi typem léčby a její úspěšností jsme neprokázali.

Závěr

I studie s malým počtem případů mají ve výzkumu své opodstatnění, zvláště tam, kde by získání většího souboru bylo příliš nákladné nebo dokonce nemožné. Pro jejich analýzu je však nutné užívat odpovídající metody založené na exaktním výpočtu dosažené hladiny významnosti.

Pokud Vás problematika exaktních testů zaujala a chcete se o ní dozvědět víc, můžeme Vám doporučit například kurz Analýza kategorizovaných dat I, kde si mimo jiné vysvětlíme podstatu Fisherova exaktního testu pro kontingenční tabulku.