Víte, jak v IBM SPSS Statistics spočítat intervaly spolehlivosti pro Pearsonův korelační koeficient?

Program IBM SPSS Statistics umožňuje spočítat tři základní typy korelačních koeficientů (Pearsonův, Spearmanovo ρ, a Kendallovo tau-b) a jejich dosažené hladiny významnosti. Někdy však potřebujete znát také jejich intervaly spolehlivosti. V tomto článku si představíme rozšiřující proceduru, která umožňuje spočítat intervaly spolehlivosti pro Pearsonův lineární korelační koeficient a případně také pro Spearmanovo ρ. Tuto proceduru si můžete zdarma stáhnout a začlenit ji do menu programu.

Korelace v IBM SPSS Statistics

Pro výpočet korelací v IBM SPSS Statistics je určena nabídka Analyze, Correlate, Bivariate, která poskytuje Pearsonův lineární korelační koeficient a dva typy neparametrických koeficientů korelace – Spearmanovo ρ a Kendallovo tau-b. Zároveň je k dispozici také test nulovosti těchto koeficientů. Kromě toho lze zobrazit kovarianční matici vstupních proměnných a některé další statistiky. Pro výpočet je možné specifikovat způsob práce s vynechanými hodnotami a typ alternativní hypotézy testu nulovosti. Rovněž lze zvolit, zda se mají označit statisticky významné korelační koeficienty a zda se má zobrazit celá korelační matice nebo jen dolní trojúhelník s diagonálou nebo bez ní. Procedura nabízí i některá rozšíření v syntaxi (například výpočet obdélníkové korelační matice nebo uložení korelační matice do souboru).

V řadě situací je však užitečné spočítat také interval spolehlivosti pro korelační koeficient. Pro tento případ je určena rozšiřující procedura STATS_CORRELATIONS, která využívá integraci programovacího jazyka Python do IBM SPSS Statistics. Umožňuje zobrazit interval spolehlivosti pro Pearsonův lineární korelační koeficient, lze ji však užít i pro Spearmanovo ρ (pokud se obě proměnné nejprve převedou na pořadí pomocí nabídky Transform, Rank Casesa do výpočtu se následně zadají takto transformované proměnné).

Softwarová rozšíření a instalace procedury STATS_CORRELATIONS

Softwarová rozšíření IBM SPSS Statistics umožňují obohatit nástroje tohoto programu díky spolupráci s programovacími jazyky Python, R nebo Java. Řada těchto rozšíření je k dispozici zdarma ke stažení, uživatelé si je však mohou vytvářet také sami a sdílet je mezi sebou. Obvykle se předávají ve formě tzv. instalačních balíčků (soubory s příponou *.spe), které mohou obsahovat kromě kódu také definici uživatelského dialogu a další komponenty.

Pro správu softwarových rozšíření je určena nabídka Extensions, Extension Hub, kde se zároveň připojíte k portálu pro sdílení těchto rozšíření mezi uživateli. Typicky se jedná o malé softwarové celky o velikosti několik kilobytů/megabytů, které snadno začleníte přímo do softwaru IBM SPSS Statistics. Aktuálně jsou k dispozici desítky až stovky takových rozšíření.  Tento dialog nabízí možnost snáze se v nich orientovat, třídit je podle zaměření, stahovat, instalovat, získat přehled o požadovaném softwarovém vybavení apod.

Pro instalaci procedury STATS_CORRELATIONS potřebujete připojení na internet. V nabídce Extensions, Extension Hub zvoltezáložku Explore, kde se automaticky načítají informace o rozšířeních, která jsou k dispozici na portálu IBM SPSS Predictive Analytics collection GitHub (https:/ibmpredictiveanalytics.github.io/). Do pole Search zadejte STATS_CORRELATIONS, zrušte všechny filtrující podmínky níže a potvrďte tlačítkem Apply. Následně se zobrazí informace o této proceduře.

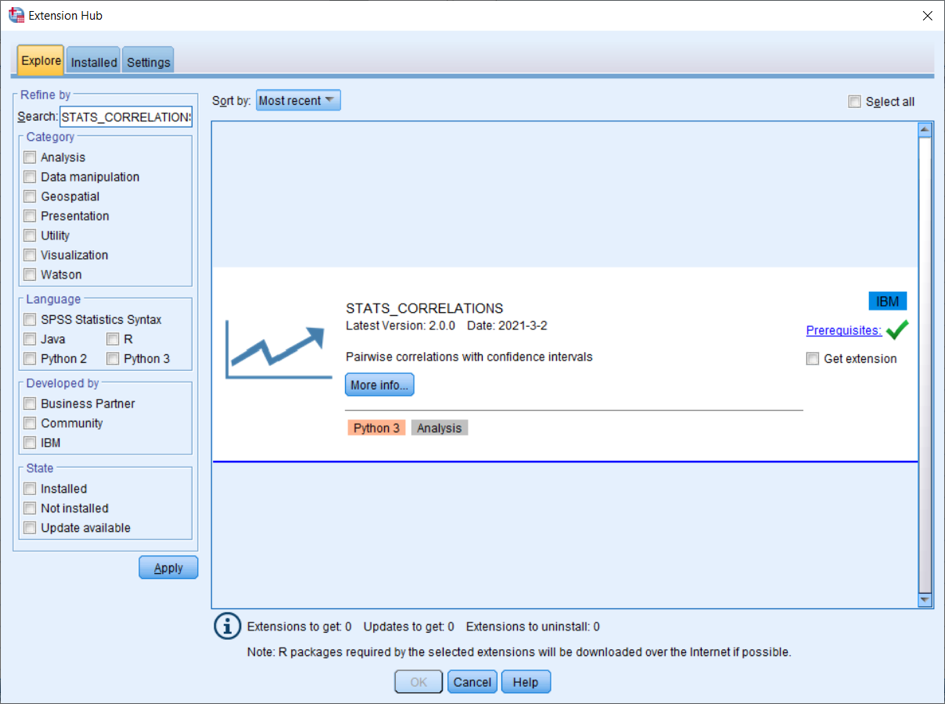
Tlačítkem More info zobrazíte podrobnosti (verze, autor, datum vydání, nejnižší a nejvyšší podporovaná verze IBM SPSS Statistics, nutný software apod.). Odkaz Prerequisites otevře okno s přehledem požadovaného softwarového vybavení. Zelený symbol vpravo značí, že vše je v pořádku a není třeba nic doinstalovat. Červený vykřičník naopak upozorňuje, že je nutné Prerequisites otevřít a zjistit, co chybí.

Procedura STATS_CORRELATIONS je k dispozici pro verzi IBM SPSS Statistics 24 nebo vyšší a vyžaduje instalaci programovacího jazyka Python a integračního pluginu pro Python. Při standardní instalaci IBM SPSS Statistics se však všechny tyto komponenty instalují automaticky (pokud tuto volbu nezrušíte) a měli byste tedy již mít vše potřebné k dispozici. Samotnou instalaci procedury STATS_CORRELATIONS provedete jednoduše označením volby Get extension a potvrzením tlačítkem OK. Během instalace je nutné ještě akceptovat licenční podmínky.

Po úspěšné instalaci se procedura začlení do menu programu, naleznete ji v nabídce Analyze, Correlate, Bivariate with Confidence Intervals.

Ukázka

Pro ukázku užijeme známý datový soubor o kosatcích (Iris), který představil R. A. Fisher ve svém článku z roku 1936. Obsahuje informace o třech druzích kosatců (setosa, versicolor a virginica). U 50 rostlin každého druhu se zjišťovala délka a šířka kališního lístku a délka a šířka korunního lístku.

Nejprve prozkoumáme vztah mezi délkou a šířkou korunního lístku bez ohledu na druh kosatce. Bodový graf naznačuje, že mezi proměnnými je poměrně silná lineární závislost. 

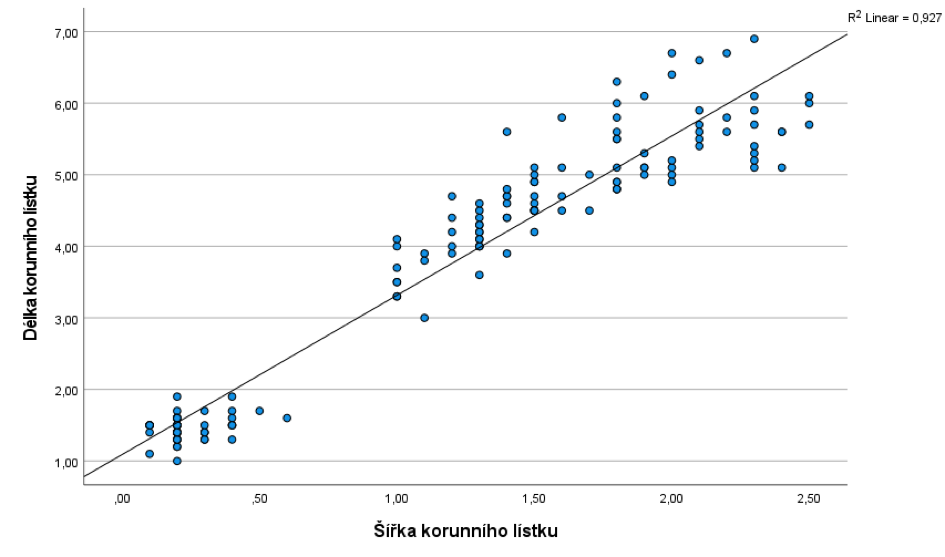
Pro výpočet Pearsonova lineárního korelačního koeficientu užijeme nejprve nabídku Analyze, Correlate, Bivariate. Hodnota korelačního koeficientu 0,963 svědčí o velmi silném vztahu mezi těmito proměnnými – čím vyšší je hodnota jedné z nich, tím vyšší je i hodnota druhé. Nízká dosažená hladina významnosti (Sig. (2-tailed)) zároveň naznačuje, že se nejedná o náhodný souběh variabilit.

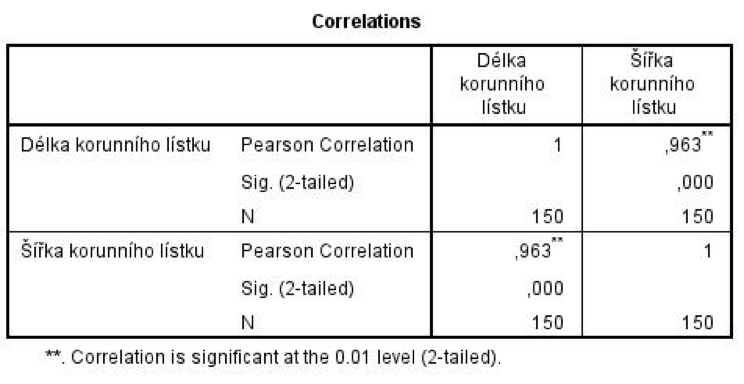
Pro výpočet intervalu spolehlivosti pro Personův korelační koeficient užijeme proceduru STATS_CORRELATIONS v nabídce Analyze, Correlate, Bivariate with Confidence Intervals.

V dialogovém okně zadáme jednu z proměnných do pole Variables a druhou do pole With Variables. V případě čtvercové korelační matice stačí přenést celou skupinu proměnných do pole Variables. Pro výpočet obdélníkové korelační matice (skupina proměnných proti jiné skupině proměnných) se proměnné rozdělí do obou polí. 

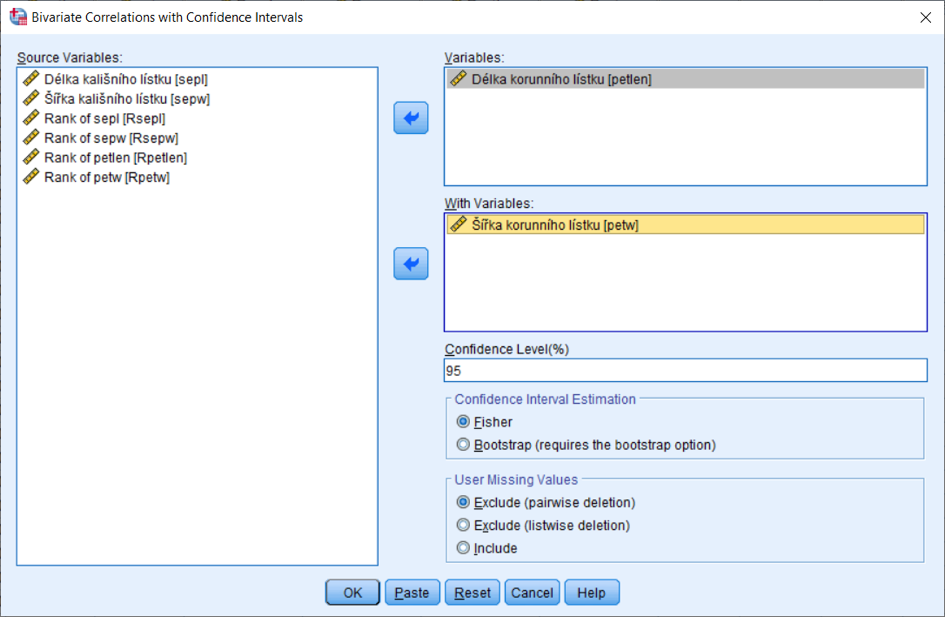
V poli Confidence Level (%) nastavíme požadovanou hladinu spolehlivosti.

V části Confidence Interval Estimationvolíme metodu odhadu intervalu spolehlivosti: na základě Fisherovy transformace s přibližně normálním rozložením, nebo pomocí metody bootstrapping (viz samostatný článek Bootstrapping – aneb jak souvisí statistika s řemínky na botách).

V oblasti User Missing Values určíme způsob práce s vynechanými hodnotami: metody pairwise, listwise, nebo zahrnutí uživatelem definovaných vynechaných hodnot do výpočtu jako platných (systémové vynechané hodnoty se vyloučí vždy).

Procedura má rovněž vlastní syntaxový příkaz, který můžete zobrazit pomocí tlačítka Paste.

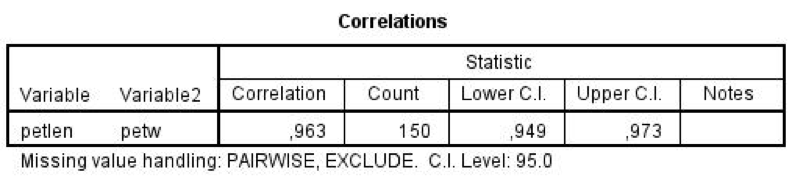
Výsledná tabulka zobrazuje názvy vstupních proměnných (vždy se zobrazují názvy nikoliv popisy) a ve sloupcích postupně naleznete: hodnotu korelačního koeficientu (Correlation), počet případů, z nichž byl vypočítán (Count), dolní mez intervalu spolehlivosti (Lower C. I.), horní mez intervalu spolehlivosti (Upper C. I.) a případně poznámky (Notes). Skutečná hodnota korelačního koeficientu by se tedy s 95% spolehlivostí měla nacházet v intervalu (0,949; 0,973).

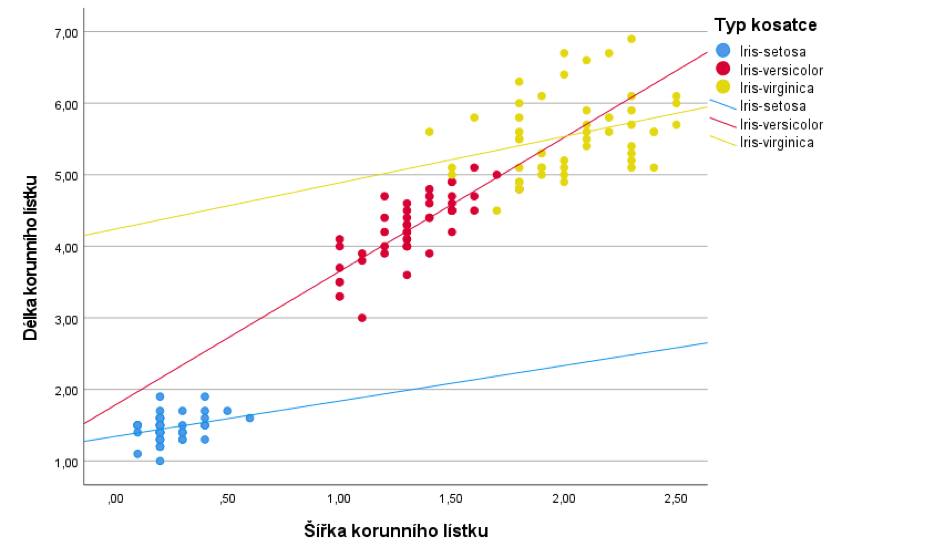
Dále se podíváme, jak by situaci vypadala, pokud bychom zkoumali každý typ kosatce samostatně. V bodovém grafu jsou jednotlivé typy odlišené barevně a zároveň je pro každý z nich zobrazena samostatná regresní přímka.

Pro výpočet korelačního koeficientu ve skupinách je třeba datový soubor nejprve rozštěpit podle typu kosatce pomocí nabídky Data, Split File.

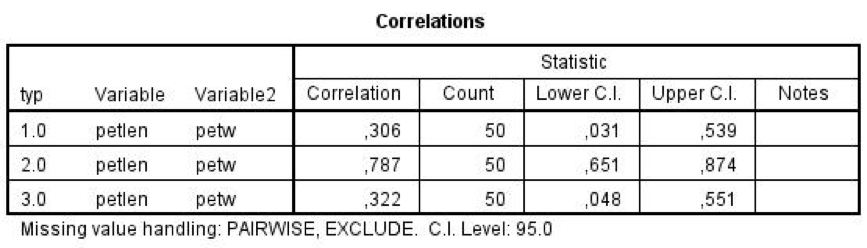
V dialogu nabídky Analyze, Correlate, Bivariate with Confidence Intervals necháme stejné zadání. Výsledná tabulka je však nyní rozdělená na tři řádky, z nichž každý odpovídá jednomu typu kosatce. Nejsilnější korelační koeficient 0,787 vychází pro druhý typ kosatce (versicolor), v ostatních skupinách je síla vztahu slabší. Ani v jednom případě však uvnitř intervalu spolehlivosti neleží nula a můžeme tedy s 95% spolehlivostí tvrdit, že se nejedná o zcela náhodný souběh variabilit. 

V této ukázce jsme pracovali s Pearsonovým lineárním korelačním koeficientem. Proceduru STATS_CORRELATIONS lze však užít i pro výpočet intervalů spolehlivosti pro Spearmanovo ρ. Tento korelační koeficient můžeme odvodit tak, že se původní proměnné nejprve převedou na pořadí a ta se následně dosadí do vzorce pro Pearsonův lineární korelační koeficient. V IBM SPSS Statistics užijeme pro tuto transformaci nabídku Transform, Rank Cases (proměnné stačí pouze přenést do poleVariables, ostatní nastavení zůstane defalutní). Nově odvozené proměnné následně zadáme do procedury STATS_CORRELATIONS. Takto získáme Spearmanův korelační koeficient původních proměnných a jeho interval spolehlivosti.

Rádi byste se o statistice a analýze dat dozvěděli více? Chcete se stát mistrem ve svém oboru nebo si jen potřebujete doplnit znalosti? V ACREA nabízíme širokou nabídku kurzů pro váš profesní růst. Máte-li jiný dotaz. Nebojte se využít naši nezávaznou konzultaci, při které vám rádi zodpovíme všechny vaše dotazy a najdeme vhodné řešení.