Analýza rozptylu a její předpoklady II

Popis metody
V minulém článku Analýza rozptylu a její předpoklady I jsme se zabývali důsledky porušeného předpokladu pro testování hypotézy o shodě středních hodnot. Článek shrnoval hlavní závěry pro klasický ANOVA test, pro robustní testy Welchův a Brownův-Forsytheův a pro neparametrický Kruskalův-Wallisův test. V tomto článku se podrobněji seznámíme s parametry simulace i jejími výsledky.
Simulace byla provedena v programu IBM SPSS Statistics 28. Byly provedeny simulace pro kombinace několika vlastností simulovaných proměnných a skupin. Vždy byly uvažovány 3 skupiny, skupiny měly buď po 20 případech nebo 10, 20 a 30 případů, výběr měl tedy vždy velikost 60 případů. Data byla generována z normálního, Laplaceova a posunutého lognormálního rozdělení. U všech rozdělení se generovala data se stejným i s rozdílným rozptylem, ve druhém případě byly směrodatné odchylky ve skupinách 1, 2 a 4. U lognormálního rozdělení se navíc uvažovala různá šikmost, ta byla ve skupinách buď stejná a to 1 nebo 3, nebo v každé rozdílná a to pak 1, 2 a 3. Pro každou kombinaci parametrů simulace bylo vygenerováno 10 000 náhodných souborů. Na nich se pak spočítaly podle vzorce teoretické signifikance ANOVA, Welchova a Brownova-Forsythova testu a Kruskalova-Wallisova testu. V základní simulaci se pro ověření správnosti signifikance uvažovala stejná střední hodnota ve skupinách. V rozšířené variantě se sledovalo i chování testů při odlišných středních hodnotách (síla testu).
Z uvažovaných rozdělení je méně známé posunuté lognormální rozdělení. Náhodná veličina Y = X – m, kde m je parametr polohy, má posunuté lognormální rozdělení, když náhodná veličina X má lognormální rozdělení. Rozšíření lognormálního rozdělení bylo nutné, aby se mohlo dosáhnout všech kombinací střední hodnoty, rozptylu a šikmosti generovaných dat. Ze zvolených kombinací střední hodnoty (pro ověření signifikance vždy 0), rozptylu a šikmosti byly spočteny parametry všech rozdělení a nasimulována data. U normálního a Laplaceova rozdělení je vztah k jejich parametrům přímočarý, u posunutého lognormálního jde o složitější soustavu rovnic, která má naštěstí explicitní řešení.
Na každém nasimulovaném výběru byly spočítány teoretické signifikance zmíněných testů. Protože testů bylo pro každou kombinaci parametrů 10 000, bylo možné přesně odhadnout skutečné (empirické) signifikance pomocí empirické distribuční funkce. Výsledky lze zobrazit několika způsoby, nejpodrobnější je vykreslit testové teoretické signifikance vůči empiricky odhadnutým. Pokud jsou předpoklady testu správné, budou si teoretické a empirické signifikance rovny a v grafu budou ležet na ose prvního kvadrantu. Pro srovnání jednotlivých kombinací parametrů simulace je vhodnější vypočítat signifikanci v jednom bodě konkrétně pro 5 %. Zatím účelem byla vytvořena proměnná typu 0–1, která nabyla hodnoty 1, pokud spočtená signifikance byla menší než 5 %. Při správnosti použití testu by měl být podíl takových testů (empirická signifikance) 5 %. Uvedený výpočet umožňuje spočítat i intervaly spolehlivosti podílu signifikantních testů.
Podrobné výsledky
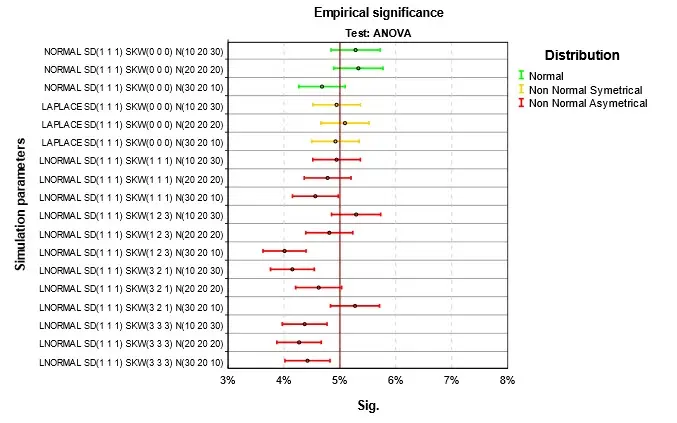
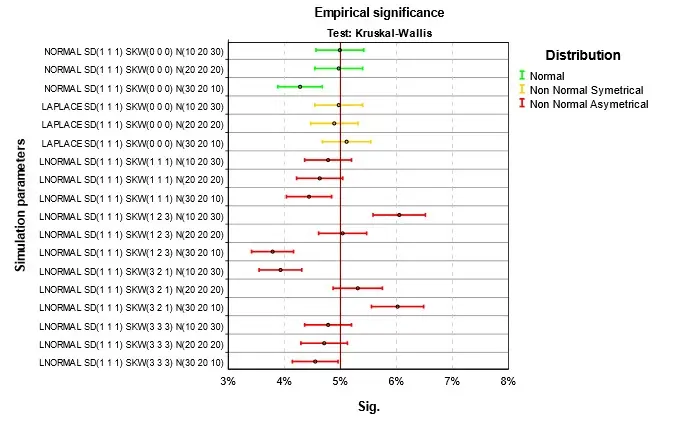
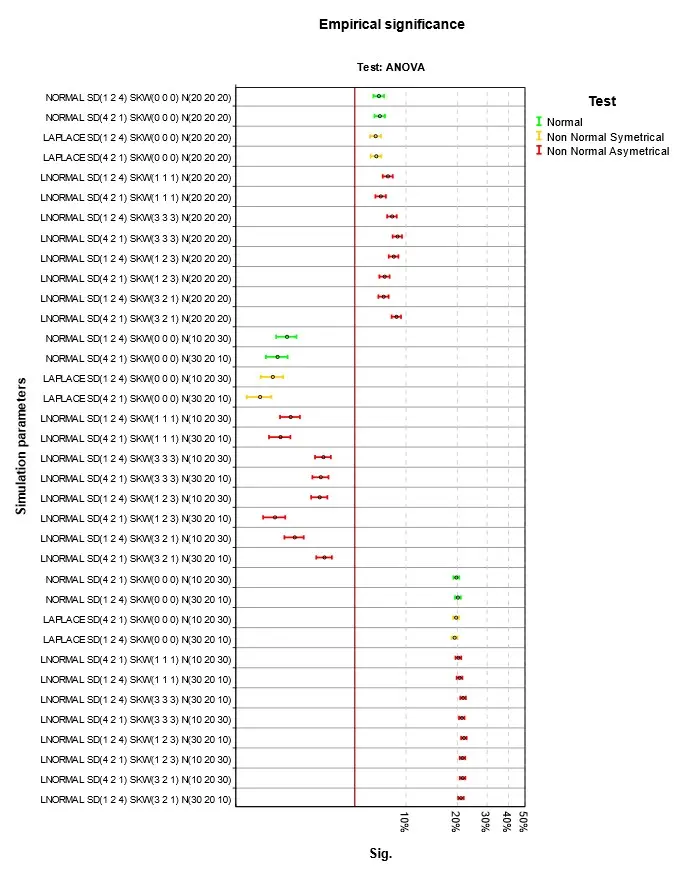
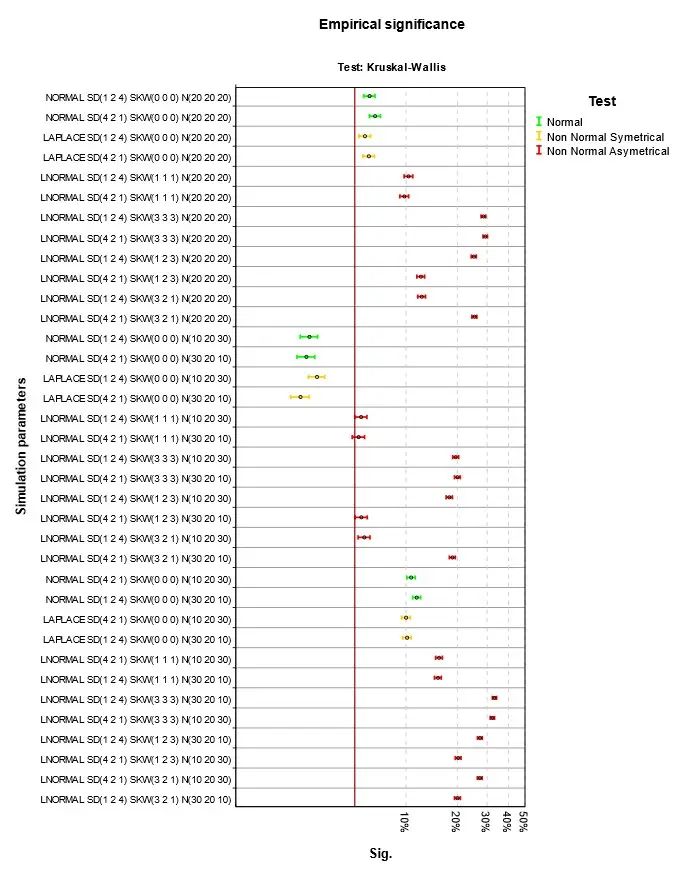
Výsledky jsou na Obr. 1 až Obr. 4. Parametry simulace jsou uvedeny v jednotném schématu. První část je typ simulovaného rozdělení, tři čísla v závorce za SD jsou směrodatné odchylky v první, druhé a třetí skupině, za SKW šikmosti a za N počty případů. Podnadpis grafu označuje druh testu. V grafu čtenář nalezne výsledky pro konkrétní parametry simulací. Empirická signifikance se příliš neliší od teoretické hodnoty 5 %. Při normalitě nebo symetrii rozdělení je situace nejlepší. Při šikmém rozdělení dosahuje nejlepších výsledků klasická ANOVA, použití robustních testů, zejména Welchova je v této situaci kontraproduktivní. Stejně málo vhodné je použít Kruskalův-Wallisův test, který je ale pro tuto situaci hojně doporučován. Při doporučení se mnohdy zapomíná na fakt, že nulová hypotéza testu není shoda středních hodnot, ale celková shoda rozdělení ve skupinách. Nulová hypotéza je zamítnuta i pokud se skupiny liší třeba rozptylem, šikmostí nebo obecně tvarem rozdělení. Jako analogie ANOVA testu se test dá použít, jen v případě, že odlišnost mezi skupinami je způsobena jen posunutím. V grafu na Obr. 4 jsou to situace, kdy se neliší ani šikmosti ve skupinách. Nejlepší výsledky pak v tomto případě Kruskalův-Wallisův test dosahuje při nenormalitě, ale to se projeví až v síle testu popisované v dalším článku Analýza rozptylu a její předpoklady III.
Obr. 1 Empirická signifikance při platnosti nulové hypotézy a homoskedasticitě – ANOVA
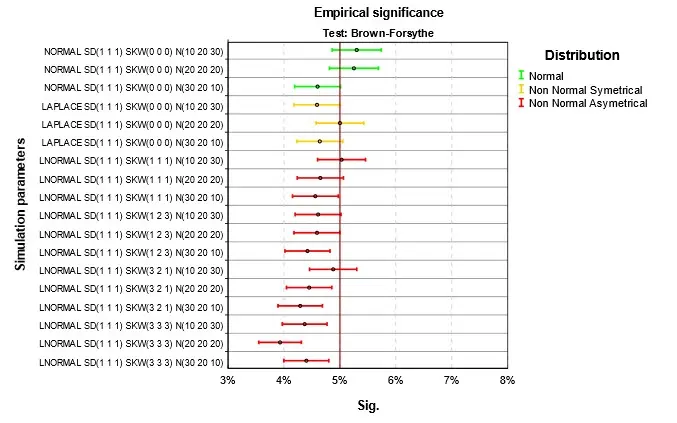
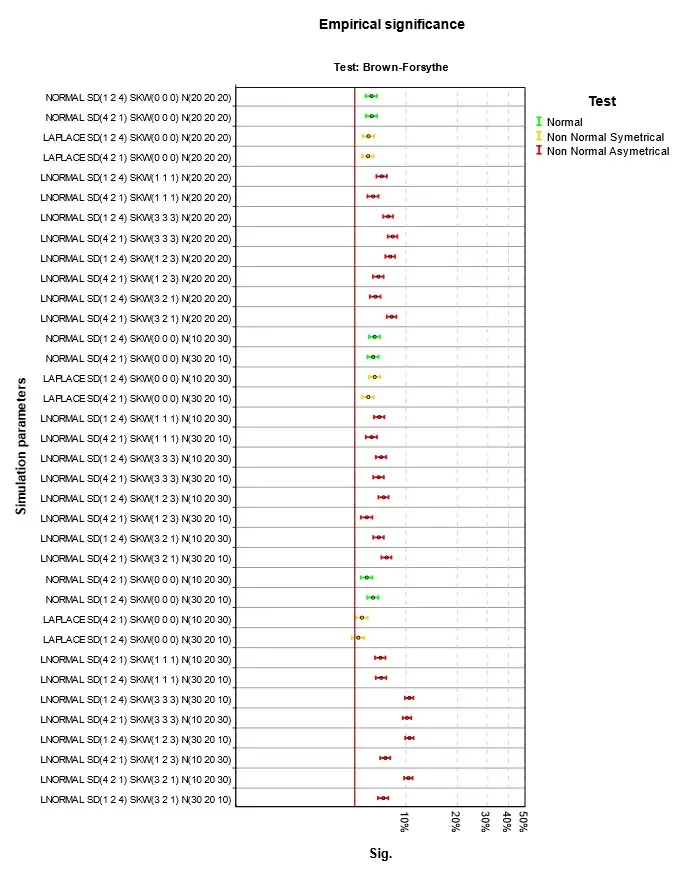
Obr. 2 Empirická signifikance při platnosti nulové hypotézy a homoskedasticitě – Brown-Forsythe
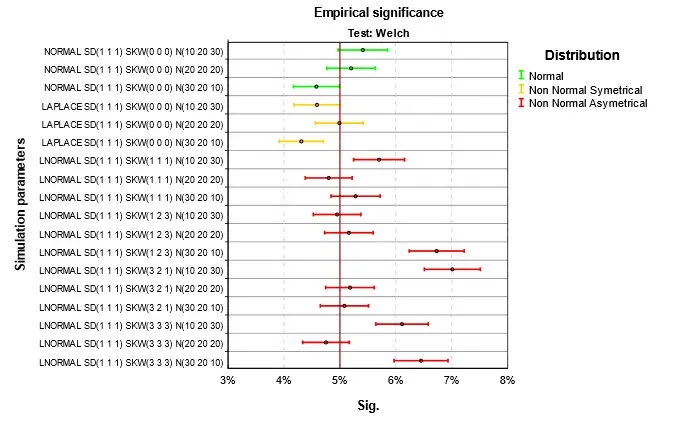
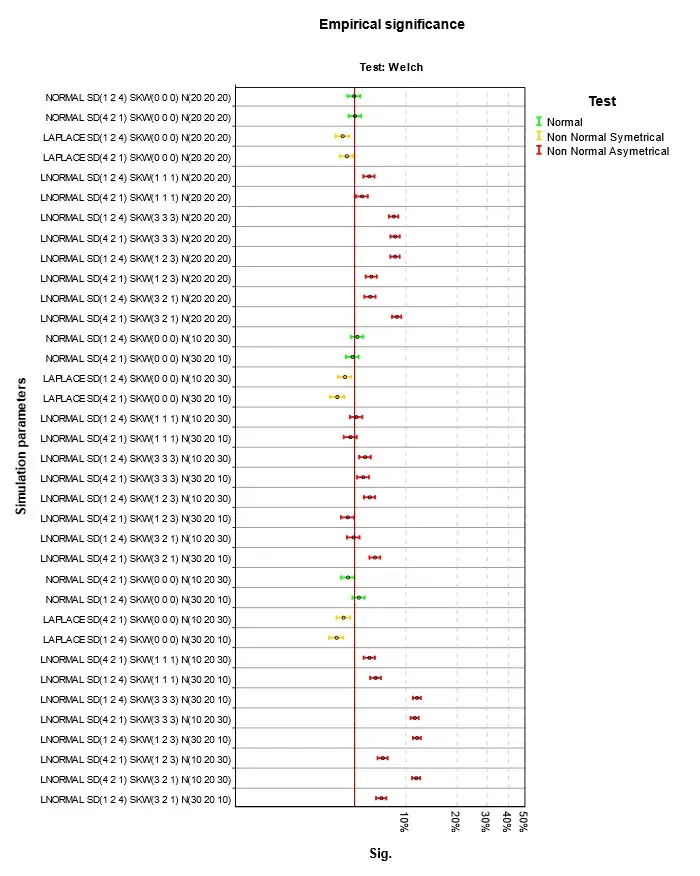
Obr. 3 Empirická signifikance při platnosti nulové hypotézy a homoskedasticitě – Welch
Obr. 4 Empirická signifikance při platnosti nulové hypotézy a homoskedasticitě – Kruskal-Wallis
Obr. 5 až Obr. 8 ukazují skutečnou signifikanci při heteroskedasticitě, kde na vodorovné ose je vynesen logaritmus empirické signifikance. Čtenář se může podívat na konkrétní parametry simulace. Celkově se dá shrnout, že nejlepších výsledků dosahují robustní testy, při normalitě nebo alespoň při symetrickém rozdělení jsou výsledky velmi dobré. Při sešikmeném rozdělení jsou horší, ale stále není nic lepšího k dispozici. Kruskalův-Wallisův test má skutečné signifikance mnohdy velmi odlišné od teoretických 5 %, což je opět důsledkem jinak formulované nulové hypotézy, než u ostatních testů.
Obr. 5 Empirická signifikance při platnosti nulové hypotézy a heteroskedasticitě – ANOVA
Obr. 6 Empirická signifikance při platnosti nulové hypotézy a heteroskedasticitě – Brown-Forsythe
Obr. 7 Empirická signifikance při platnosti nulové hypotézy a heteroskedasticitě – Welch
Obr. 8 Empirická signifikance při platnosti nulové hypotézy a heteroskedasticitě – Kruskal-Wallis
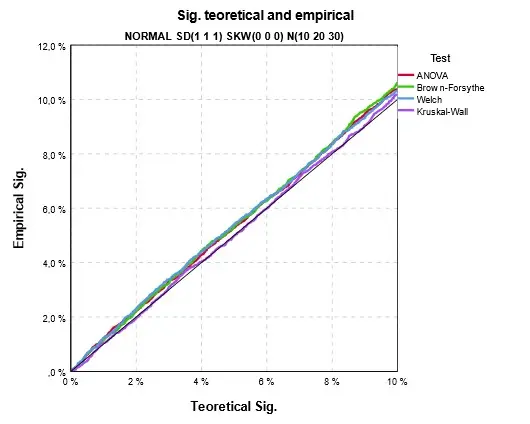
Pohled na chování testů pro 5 % hladinu významnosti jsou jen jedním, i když nejdůležitějším pohledem na dosažené signifikance. Podrobnější pohled nabízí již zmíněné srovnání teoretické a empirické distribuční funkce. Na Obr. 6 je ukázka grafu srovnávající distribuční funkce při splnění předpokladů analýzy rozptylu. Není překvapením, že teoretická funkce, spočtená podle vzorce, odpovídá v tomto ideálním případě empirické funkci. Shodu funkcí představuje černá linie, osa prvního kvadrantu.
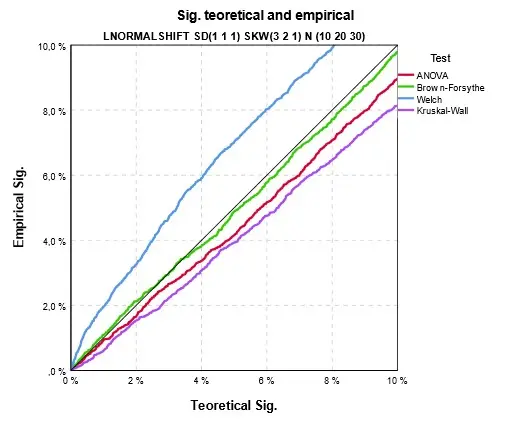
Odlišná je situace pro sešikmené rozdělení ale se stejnými rozptyly. Na Obr. 7 je shoda rozptylů sice zachována, ale rozdělení je sešikmené, a navíc skupiny obsahují různý počet případů. Hodnoty pod linií shody znamenají, že skutečná (empirická) signifikance je menší než spočtená a naopak. Z grafu je patrné, že kromě Welchova testu je spočtená signifikance větší a test je konzervativní. Welchův test má v této situaci naopak ve skutečnosti vyšší hodnotu signifikance, než udává jeho vzorec. Místo 5 % je signifikance asi 7 % a aby byla skutečná signifikance 5%, musí test vyjít se signifikancí asi 3 %. Rozdíly jsou ale i u nejhoršího Welchova testu celkem nevelké. Opět se ukazuje, že nenormalita dat není příliš velikým problémem.
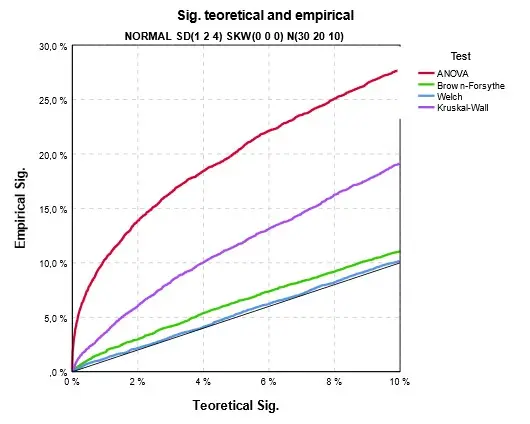
Zcela jiná situace nastává u heteroskedasticity, a to i když je zachována normalita dat. (Obr. 8). Zatímco u robustních testů vychází signifikance podle vzorce správně, u klasického testu ANOVA a také u Kruskalova-Wallisova testu je empirická signifikance výrazně odlišná od vypočtené. V tomto konkrétním případě je skutečná signifikance vyšší a test může chybně zamítnout nulovou hypotézu, např. u ANOVA testu je skutečná signifikance 20 % a podle vzorce vychází 5 %. Obecně nelze říci, zda test signifikanci nadhodnocuje nebo podhodnocuje.
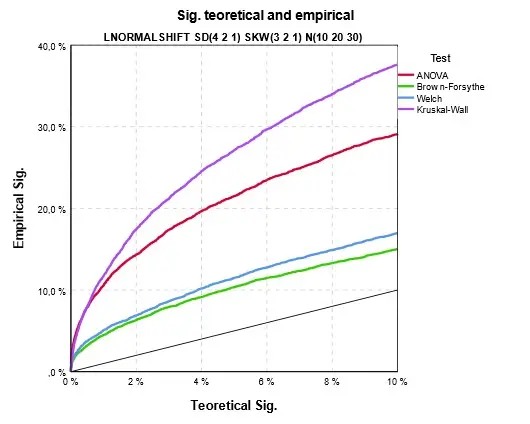
Nejhorší kombinace je tehdy, když je s heteroskedasticitou spojena výrazná a navíc různá šikmost ve skupinách. Z předchozího článku Analýza rozptylu a její předpoklady I víme, že v tomto případě neexistuje uspokojivá volba testu. Obr. 12 to potvrzuje, v tomto případě je skutečná signifikance vždy vyšší. Nejmenší rozdíl je u robustních testů, ale např. klasická ANOVA dosahuje 20 % místo spočtených 5%. K této situaci je třeba přistoupit pragmaticky. V bodě, kdy je skutečná signifikance robustních testů 5 %, vychází u nich signifikance asi 3 %. Pokud je tedy signifikance nízká např nižší než 0,01%, je velmi nepravděpodobné, že skutečná by byla nad 5 %. V praxi se často stává, že vypočtená signifikance nabývá extrémně nízkých hodnot, pak můžeme považovat výsledky testu za správné i při nepříznivých kombinacích. Vždy je ale vhodné použít test, který je zkreslen nejméně.
Uvedené průběhy empirické a teoretické distribuční funkce jsou jen ukázkou, analogické grafy se dají zkonstruovat pro všechny kombinace parametrů simulace. Pro jejich množství je zde nelze uvést.
Obr. 9 Empirická a teoretická distribuční funkce signifikance při homoskedasticitě a normálním rozdělení
Obr. 10 Empirická a teoretická distribuční funkce při homoskaeasticitě a sešikmeném rozdělení
Obr. 11 Empirická a teoretická distribuční funkce při heteroskedasticitě a normálním rozdělení
Obr. 12 Empirická a teoretická distribuční funkce při heteroskedasticitě a sešikmeném a rozdělení
Rádi byste se o statistice a analýze dat dozvěděli více? Chcete se stát mistrem ve svém oboru nebo si jen potřebujete doplnit znalosti? V ACREA nabízíme širokou nabídku kurzů pro váš profesní růst. Máte-li jiný dotaz. Nebojte se využít naši nezávaznou konzultaci, při které vám rádi zodpovíme všechny vaše dotazy a najdeme vhodné řešení.




