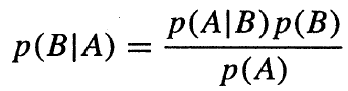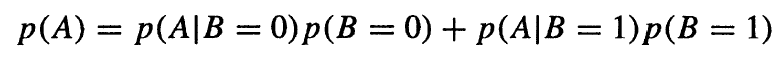Bayesovská analýza dat

Baeysovská statistika má své kořeny poměrně hluboké a dávné. Vždyť slavné pojednání reverenda Bayese (1763), které obsahuje Bayesův teorém vyšlo již před více než 250 lety. Od té doby lze datovat rozvoj statistiky, které dnes říkáme dle jejího zakladatele bayesovská či pouze bayesiánství. Zatímco základní myšlenka byla prostá a bylo možné jí teoreticky dále rozvíjet (což se dělo), aplikace bayesovských přístupů na empirická data byla obtížná, v některých případech nemožná. Tyto aplikace umožnil až rozvoj moderní výpočetní techniky a příslušných výpočetních algoritmů založený na simulacích. Druhá větev statistiky by mohla nést jméno fisherovská, ale to se používá jen okrajově, mnohem častější je výraz frekvenční či četnostní statistika[1].
Každý je Bayesiánec (aneb Bayes v našich životech)
Nadpis této části může mnohé překvapit. Zkusme si na příkladu z reálného života ukázat, že koncepce bayesovské statistiky se běžně uplatňuje v našich životech a je nám de facto vlastní. Představme si, že jdeme na setkání s neznámým člověkem. Rádi bychom vedli odbornější konverzaci na úrovni složitosti, která by odpovídala vzdělání tohoto jedince, které ovšem neznáme. Můžeme pouze využít znalosti statistických údajů (vzdělání bez maturity má 25 % osob, maturitní 55 % a zbylých 20 % má vysokoškolské vzdělání). Tuto základní informaci nazýváme apriorní informací případně ve statistice apriorním rozdělením, protože na vzdělání statistik nahlíží jako na proměnnou a každou proměnnou lze popsat jejím zákonem rozdělení. Pokud například víme, že dotyčný je ve věku 30 let, lze tuto informaci využít a rozdělení vzdělání bude jiné (podmíněné znalostí věku) a vysokoškoláků bude již např. 35 %. Obdobně budu-li mít znalost, že oba rodiče neznámého mají vysokoškolské vzdělání, zjistím ze vzdělanostních výzkumů (nebo prostou intuicí), že pravděpodobnost, že dotyčný bude mít sám vysokoškolské vzdělání je již 60 %. Dodejme, že s neznámým v takové situaci začneme nejspíše mluvit komplikovaněji a teprve, když zjistíme, že nejspíš není absolventem vysoké školy svůj slovník přizpůsobíme[2]. Dodejme, že úvodní ilustrace je záměrně zjednodušená jen na koncepci tzv. podmíněné pravděpodobnosti, pravověrné bayesiánství jde dále a snaží se „překlápět“ podmíněné pravděpodobnosti. Tj. například při znalosti pravděpodobnosti, že dítě má VŠ vzdělání, pokud jej mají rodiče (plus dalších informací, srov,. dále), budu schopen dopočítat pravděpodobnost VŠ vzdělání rodičů za podmínky, že VŠ má jejich dítě.
Právě představený koncept aktualizace pravděpodobnostních rozdělení skrze další informace je základem Bayesovské statistiky. Vycházíme z nějaké apriorní informace (lepší či horší dle její dostupnosti a naší snahy) a tu doplňujeme empirickými daty a získáme tzv. aposteriorní rozdělení námi sledované veličiny. Navíc naše výsledky (aposteriorní rozdělení) se stávají apriorními informacemi pro další výzkumníky. Dochází tak ke kumulaci informací z našich dat a předchozích výsledků. Zde vidíme základní rozdíl mezi Bayesovským a frekvenčním přístupem. Bayesovská statistika je kombinací informace dříve známé a informace získané z našich dat, která analyzujeme. Frekvenční statistika využívá pouze informace z našich aktuálních dat.
Bayesův vzorec a jeho použití na jednoduchém příkladu (Co lze z Bayese spočítat bez software?)
Pro serióznější představení Bayesovského přístupu rekapitulujeme základní poučku tzv. Bayesův vzorec (teorém). Jde o formální vyjádření představené myšlenky, tj. postupu, jak z apriorních informací doplněných našimi daty lze získat aposteriorní informaci. Prvním konceptem, který si musíme představit je podmíněná pravděpodobnost. Jde o pravděpodobnost, jejíž hodnota záleží na nějaké podmínce. Podmíněnou pravděpodobností je například zmíněná pravděpodobnost, že dotyčný je vysokoškolák, za podmínky, že víme, že jeho rodiče mají VŠ vzdělání (případně má 30 let). Formálně zapisujeme nepodmíněnou pravděpodobnost nějakého jevu (pro náhodné jevy většinou užíváme velká písmena z počátku abecedy) P(A), podmíněnou pravděpodobnost zapisujeme P(A/B), kde A značí jev, který nás zajímá (například vzdělání jedince) a B podmínku (například skutečnost, že rodiče mají VŠ vzdělání).
Bayesův vzorec pak umožňuje v případě, že známe pravděpodobnost jevu B (apriorní) a podmíněnou pravděpodobnost jevu A za podmínky B (výsledek našich dat), stanovit podmíněnou pravděpodobnost jevu B za podmínky výskytu jevu A. Formálně vypadá Bayesův vzorec následovně:
Pro výpočet potřebujeme znát podmíněnou pravděpodobnost jevu A za podmínky B, pravděpodobnost jevu B a pravděpodobnost jevu A (tzv. úplnou pravděpodobnost). Úplnou pravděpodobnost jevu A lze určit ze vzorce:
Abychom přispěli k pochopení vzorce, uveďme jednoduchý příklad[3]. Představme si, že příslušnou diagnózu má v populaci 5 % osob. Formálně tento jev označme písmenem B, tj. P(B=1) = 0,05. Diagnostický postup (jev A), který se používá v medicíně odhalí nemoc s pravděpodobností 0,85, tj. P(A/B=1) = 0,85 (daný ukazatel bývá zvykem označovat TPR, tj. True Positive ratio, neboli poměr správně diagnostikovaných) . Dále předpokládejme, že diagnostický postup chybně diagnostikuje chorobu pro zdravého v 15 % případů (formálně zapsáno P(A/B=0) = 0,15). Tento ukazatel bývá zvykem označovat FPR, tj. False Positive ratio, neboli poměr chybně diagnostikovaných. Snadno též dopočteme, že P(B=0) = 0,95, tj. chorobou v populaci netrpí 95 % (doplněk 5% nemocných do 100 %). Nyní již tedy můžeme odpovědět klíčovou otázku. Jaká je pravděpodobnost, že mám příslušnou diagnózu za podmínky, že výsledek vyšetření byl pozitivní, tj. hledáme hodnotu P(B/A). To je otázka, která mne totiž typicky zajímá (Mám pozitivní vyšetření, jaká je pravděpodobnost, že jsem opravdu nemocen?)
Dosadíme postupně do vzorců, nejdříve spočteme úplnou pravděpodobnost P(A) dle vzorce 1.2:
P(A)=0,185
Jde o úplnou (celkovou) pravděpodobnost pozitivního výsledku, tj. 18, 5 % vyšetřených je sdělen pozitivní výsledek.
Poté spočteme kýženou pravděpodobnost nemoci za podmínky, že vyšetření bylo pozitivní dle vzorce 1.1:
P(B/A) = (0,85*0,05)/ 0,185 = 0,23.
Překvapení je tedy na světě, i když výsledek diagnostiky (poměrně spolehlivé) je pozitivní, pravděpodobnost, že jsme opravdu nemocní je necelá čtvrtina. Je patrné, že znalost Bayesova vzorce nám může ušetřit mnohé psychické stresy v ambulancích lékařů, ale jak jsme již předestřeli výše, může nám pomoci i v běžném sociálním životě.
Zdůrazněme zde základní rys bayesiánství v našem příkladu. Když jdeme do ordinace, máme apriorní pravděpodobnost nemoci 0,05 (tj. míru prevalence choroby v populaci). Poté dojde k aktualizaci této pravděpodobnosti skrze data (naše vyšetření). A pokud je naše vyšetření pozitivní, pak se pravděpodobnost choroby aktualizovala na 23 % (tedy cca 4,5x vyšší než na počátku). Na základě apriorní pravděpodobnosti a dat, tak můžeme dopočítat aposteriorní pravděpodobnost. Dodejme, že z výzkumů prováděných na lékařích a laické veřejnosti je známo, že dochází k častému obracení pravděpodobností. Tj. pokud např. víme, že pravděpodobnost že přístroj odhalí nemoc s pravděpodobností 0,8 (pokud ji máme), míváme tendenci si myslet, že když je vyšetření pozitivní, máme nemoc s 80% pravděpodobností. To ale jak jsme ukázali na našem příkladu není pravda, zjednodušeně formálně zapsáno obecně neplatí P(B/A)= P(A/B).
V praxi používáme bayesovskou statistiku pro složitější úlohy. Můžeme ji využít například pro srovnání průměrů ve dvou skupinách (typicky řešené ve frekvenční statistice skrze t-testy), více skupinách (typicky řešené analýzou rozptylu), souvislosti spojitých proměnných (typicky řešíme skrze korelace či regrese). Všechny tyto úlohy lze nyní bayesovsky řešit i v SPSS. Právě tomu je věnován kurz Úvod do bayesovské analýzy.
[1] V češtině není ani jeden z překladů anglického výrazu „frequentism“ ustálen, používáme proto převzatého výrazu frekvenční statistika.
[2] Samozřejmě se nabízí mnoho aplikací z oblasti karetních či hazardních her. Tyto příklady pro jejich hojné užívání vynecháváme.
[3] Volíme oblíbené příklady z medicíny. Důvody jsou minimálně dva. Prvním je skutečnost, že každý z nás se v životě potkává z různými vyšetřeními a pozitivní výsledky nás děsí (často neoprávněně). Druhým důvodem je velká oblíbenost a snadná srozumitelnost těchto příkladů.
Rádi byste se o statistice a analýze dat dozvěděli více? Chcete se stát mistrem ve svém oboru nebo si jen potřebujete doplnit znalosti? V ACREA nabízíme širokou nabídku kurzů pro váš profesní růst. Máte-li jiný dotaz. Nebojte se využít naši nezávaznou konzultaci, při které vám rádi zodpovíme všechny vaše dotazy a najdeme vhodné řešení.