Medzné efekty v logistickej regresii – užitočná interpretácia výsledkov logistickej regresie

Okrem bežne používanej interpretácie výsledkov logistickej regresie pomocou logitu, šance prípadne pomeru šancí existuje aj menej známa avšak pomerne často využívaná (najmä v oblasti ekonomických aplikácií) interpretácia pomocou medzných efektov. Mnoho účastníkov nášho kurzu logistickej regresie sa nás zvykne pýtať na medzné efekty v logistickej regresii a ako je možné ich vypočítať v softvéri IBM SPSS Statistics. V tomto článku si preto tieto časté a nie jednoduché otázky zodpovieme a vysvetlíme. Začneme však vysvetlením medzných efektov v lineárnej regresii.

Medzné efekty v lineárnej regresii

Rovnica lineárneho regresného modelu je v tvare

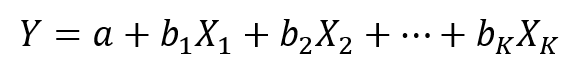
Medzným (marginálnym) efektom v lineárnej regresii máme na mysli o koľko sa nám zmení závislá premenná Y pri malej zmene nejakej nezávislej premennej X za predpokladu, že ostatné nezávislé premenné sa nemenia. To znamená, že pre každú nezávislú premennú chceme poznať jej medzný efekt. K zisteniu jednotlivých medzných efektov môžeme zvoliť dva prístupy. Prvý prístup je pomocou parciálnej derivácie premennej Y podľa X_i, formálne teda

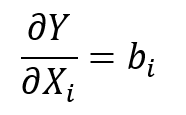
a druhý cez zmenu nejakej nezávislej premennej o jednotku (napríklad X₁)

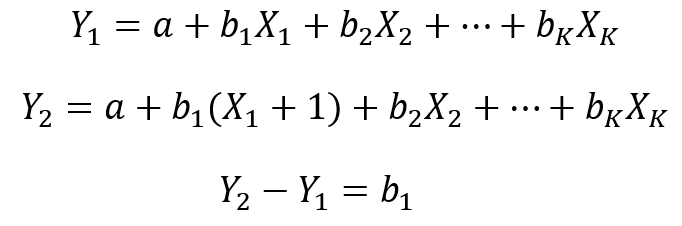
Pri obidvoch prístupoch dostaneme zhodné medzné efekty. Medzný efekt X_i na Y v lineárnej regresii je rovný práve regresnému koeficientu b_i. Interpretujeme ho teda tak, že o koľko sa zmení závislá premenná Y ak nezávislá premenná X_i sa zmení o jednotku a ostatné nezávislé premenné sa nezmenia.

Medzné efekty v logistickej regresii

Rovnica binárneho logistického modelu je v tvare

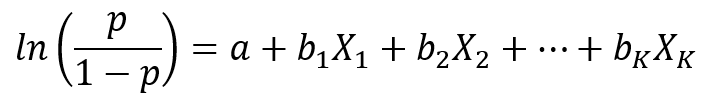
Ak by sme uvažovali medzný efekt X_i na logit, t.j. ln(p/(1-p)), závery z lineárnej regresie ostávajú v platnosti. Avšak nás zaujíma skôr medzný efekt na pravdepodobnosť výskytu udalosti

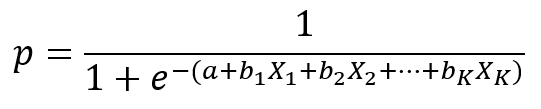
To znamená, o koľko sa zmení pravdepodobnosť výskytu nami sledovaného javu pri malej zmene nejakej nezávislej premennej X a nemennosti ostatných nezávislých premenných. Ak by sme zvolili prístup pomocou zmeny o jednotku (napríklad X₁), medzný efekt nie je jasný (mení sa v závislosti od hodnôt X)

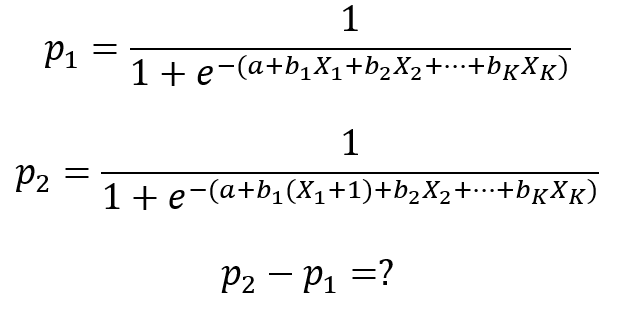
Je to z toho dôvodu, že závislosť p od hodnôt X nie je lineárna. Jednotková zmena pre nejakú nezávislú premennú X neprodukuje stále rovnakú zmenu p.

Ak by sme zvolili prístup pomocou parciálnej derivácie

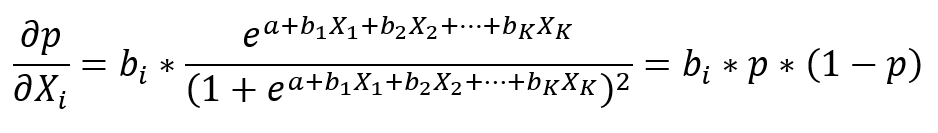
Medzný efekt X_i na p opäť nie je jasný (mení sa v závislosti od hodnôt X), pretože závislosť p od hodnôt X nie je lineárna.

Rôzne typy medzných efektov v logistickej regresii

Vzhľadom na nejednoznačnosť medzných efektov v logistickej regresii, existuje viacero možností ako ich vypočítať a následne interpretovať. Najčastejšie bývajú v softvéroch implementované dva typy medzných efektov vychádzajúce z prístupu pomocou parciálnej derivácie. Prvý je Sample Average Marginal Effects, ktorý sa počíta ako

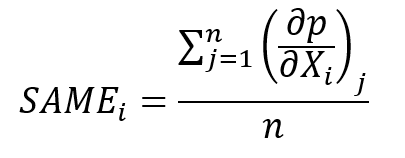
To znamená, že sa pre každý prípad v dátovej matici sa vypočíta parciálna derivácia funkcie pravdepodobnosti podľa nezávislých premenných a následne spriemeruje. Interpretujeme to tak, že pri malej zmene nezávislej premennej X_i (o jednotku) a nemennosti ostatných nezávislých premenných sa pravdepodobnosť zmení v priemere o hodnotu SAME_i.

Druhý typ medzného efektu je Marginal Effects at the Mean, ktorý sa počíta ako

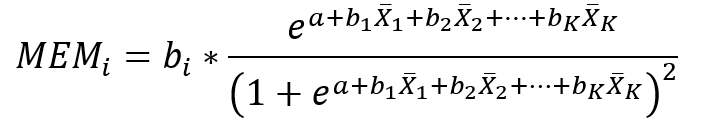
Teda využíva sa parciálna derivácia funkcie pravdepodobnosti podľa nezávislých premenných avšak následne sa za nezávislé premenné dosadia ich priemerné hodnoty. Výpočty priemerov nezávislých premenných sa môžu líšiť v závislosti od toho aký zvolíme prístup so zaobchádzaním vynechaných hodnôt. Buď sú počítané ako listwise (MEML_i) alebo pairwise (MEMP_i). Tento typ medzného efektu interpretujeme tak, že pri malej zmene nezávislej premennej X_i (o jednotku) a nemennosti ostatných nezávislých premenných, ktoré sú na svojich priemeroch (vrátane X_i), sa pravdepodobnosť p zmení o hodnotu MEM_i.

Tretí typ medzného efektu vychádzajúceho z prístupu pomocou zmeny o jednotku je Sample Average Marginal Effects (1 unit change)

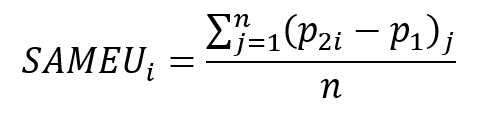
To znamená, že pre každé pozorovanie sa vypočíta pravdepodobnosť výskytu udalosti na základe jeho hodnôt pre nezávislé premenné (p₁) a pravdepodobnosť s o jednu jednotku vyššou hodnotou pre nezávislú premennú, pre ktorú medzný efekt počítame (p_2i). Následne sa spočíta ich rozdiel a spriemeruje za všetky pozorovania. Interpretujeme to tak, že pri zmene nezávislej premennej X_i o jednotku a nemennosti ostatných nezávislých premenných sa pravdepodobnosť p zmení v priemere o hodnotu SAMEU_i.

Posledný typ medzného efektu, ktorý si uvedieme je Marginal Effects from Linear Regression

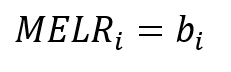
Jedná sa teda o medzný efekt, ktorý priamo odpovedá regresnému koeficientu z lineárnej regresie. Interpretujeme to tak, že pri zmene nezávislej premennej X_i o jednotku a nemennosti ostatných nezávislých premenných sa pravdepodobnosť p zmení v priemere o hodnotu MELR_i. Niektorí ekonometri ho pre porovnanie s ostatnými typmi medzných efektov a v prípade publikácie lineárneho regresného modelu aj pre dichotomickú (0/1) závislú premennú zvyknú tiež využívať. Avšak treba si uvedomiť, že nie sú splnené predpoklady modelu lineárnej regresie.

Príklad

V softvéri IBM SPSS Statistics nie sú vyššie uvedené medzné efekty vychádzajúce z binárnej logistickej regresie implementované. Preto spoločnosť ACREA vytvorila užívateľskú procedúru (Medzné efekty v logistickej regresii), pomocou ktorej sú ľahko dostupné vo forme tabuľky vo výstupe.

Pre ukážku budeme uvažovať zamestnancov banky, ktorí rozhodujú o schválení resp. zamietnutí žiadostí o úver a chcú poznať okrem charakteristík, ktoré indikujú vyššiu pravdepodobnosť problémov pri splácaní úveru, aj ich medzné efekty.

Dátový súbor obsahuje informácie o minulých zákazníkoch. O každom zákazníkovi sú k dispozícii rozličné informácie ako vek v rokoch (age), počet rokov u súčasného zamestnávateľa (employ), dĺžka pobytu na súčasné adrese v rokoch (address), podieľ dlhu k príjmu (x100) (debtinc), dlh na kreditnej karte v tisícoch (creddebt) atď. a samozrejme informácia o tom, či nastali problémy so splácaním úveru (default).

Pomocou logistickej regresie (Analyze ® Regression ® Binary Logistic…) sme najskôr identifikovali charakteristiky, ktoré sú významné pre predpoveď problémov so splácaním a následne využili procedúru Medzné efekty v logistickej regresii. Konkrétne age, employ, debtinc a creddebt.

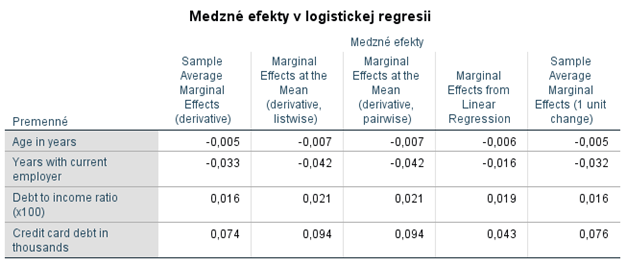
V tabuľke Medzné efekty v logistickej regresii máme medzné efekty (stĺpce) pre jednotlivé nezávislé premenné (riadky) v modeli logistickej regresie.

Na základe prvého stĺpca vieme napríklad povedať, že pri malej zmene nezávislej premennej Age in years (zvýšenie o jeden rok) a nemennosti ostatných nezávislých premenných sa pravdepodobnosť defaultu zníži v priemere o 0,005. V percentuálnom vyjadrení to znamená pokles v priemere o 0,5 percentuálneho bodu. Pre premennú Debt to income ration (x100) sa pravdepodobnosť v priemere zvýši o 1,6 percentuálneho bodu. Hodnoty medzných efektov v jednotlivých riadkoch však z dôvodu rozdielnych škál nie je možné porovnávať.

Ak sa pozrieme na prvý a posledný stĺpec, výsledky sú takmer totožné.

Výsledky v druhom a treťom stĺpci sú úplne totožné. To je z toho dôvodu, že dátový súbor neobsahoval žiadne vynechané hodnoty a teda sa nelíšia priemery nezávislých premenných so zaobchádzaním s vynechanými hodnotami ako listwise alebo stepwise. Tieto medzné efekty by sme interpretovali napríklad pre premennú Credit card debt in thousands tak, že pri malej zmene tejto premennej (zvýšenie o 1, t.j. 1 000 dolárov väčší dlh na kreditnej karte) a nemennosti ostatných nezávislých premenných, ktoré sú na svojich priemeroch (vrátane Credit card debt in thousands), sa pravdepodobnosť defaultu zvýši o 0,094. V percentuálnom vyjadrení to znamená nárast o 9,4 percentuálneho bodu.

Ak by niekto predsa len preferoval model lineárnej regresie, v štvrtom stĺpci sú medzné efekty pre jednotlivé nezávislé premennú z modelu lineárnej regresie. Pre premenné Years with current employer a Credit card debt in thousands sú oproti iným medzným efektom viditeľné najväčšie rozdiely.

Kategorické nezávislé premenné

V prípade, že logistická regresia obsahuje aj kategorické nezávislé premenné, situácia sa trocha komplikuje. Najjednoduchšie je, že sa kategorické premenné prevedú na indikátory (0/1 premenné) s jednou kategóriou ako referenčnou (v procedúre poslednou) a následne, keď sa zahrnú do regresie, pracuje sa s nimi ako s číselným premennými a teda postup a medzné efekty sú rovnaké ako je vyššie popísané. Medzný efekt pre príslušný indikátor (kategóriu) potom vyjadruje rozdiel pravdepodobnosti oproti referenčnej kategórii. Takto je to aj aplikované v našej procedúre.

Avšak existujú aj iné možnosti ako počítať medzné efekty pre kategorické premenné. Keďže chceme vedieť o koľko sa zmení pravdepodobnosť pokiaľ prejdeme z referenčnej kategórie na konkrétnu jednu, tak môžeme napríklad počítať priemernú pravdepodobnosť pre referenčnú kategóriu (na základe výberového súboru) a priemernú pravdepodobnosť pre kategóriu, ktorá nás zaujíma a následne tieto dve priemerné hodnoty odčítať.

Ďalšia možnosť môže byť ísť priamo cez funkciu pravdepodobnosti, keďže pre nejakú kategóriu kategorickej premennej sú indikátory pre ostatné kategórie danej kategorickej premennej rovné nula. Potrebné je však dosadiť za nezávislé premenné ich priemery. Spočíta sa teda pravdepodobnosť referenčnej kategórie a pravdepodobnosť kategórie, ktorá nás zaujíma a následne sa tieto dve pravdepodobnosti odčítajú. Problém však nastáva, ak máme viac kategorických premenných v modeli. Potom buď za indikátory dosadíme ich priemerné hodnoty (takto to je aplikované aj v našej procedúre), alebo pristúpime k tomu trochu inak. Spočítame pravdepodobnosti vo všetkých triedeniach (kombináciách kategórií) a následne spriemerujeme pre kategórie kategorickej premennej, ktorá nás zaujíma. Potom už len odčítavame pravdepodobnosť kategórie, ktorá nás zaujíma a pravdepodobnosť referenčnej kategórie. Takýmto princípom to robí aj IBM SPSS Statiscs v procedúre Generalized Linear Models s tým rozdielom, že počíta priemerné logity, ktoré potom transformuje na pravdepodobnosť. Vo výstupnej tabuľke sú tam pre jednotlivé kategórie buď hodnoty logitov alebo pravdepodobností, podľa toho čo užívateľ požaduje. Príslušné rozdiely pravdepodobností si už užívateľ musí spraviť sám.

Ktoré typy medzných efektov použiť

Na to, ktorý typ medzného efektu kedy použiť, neexistuje žiadne presné pravidlo a jednotný názor. Skôr preferencia užívateľa prípadne zaužívanie v odbore. Preto je ich v procedúre viac (najbežnejšie používané) a to by sa ešte dali vymyslieť aj ďalšie (pozri časť kategorické nezávislé premenné).

Ak sa bavíme o preferencii medzných efektov pre číselné premenné, niektoré štatistické programy používajú SAME_i a niektoré MEM_i alebo poskytujú oboje. SAME_i má jasnejšiu a krajšiu interpretáciu, pretože vyjadruje o koľko v priemere sa zvýši pravdepodobnosť (na základe výberového súboru) a nefixujú sa nezávislé premenné na ich priemeroch. Medzi MEML_i a MEMP_i by preferencia skôr padla na MEML_i, pretože odhad regresných koeficientov a následne aj medzných efektov (priemery) vychádzajú z listwise. SAMEU_i je ekvivalent prístupu z lineárnej regresie avšak aplikovaný na logistickú. V praxi nie je veľmi využívaný. Má však jasnú interpretáciu. Najmenej vhodná sa pre číselné premenné zdá lineárna regresia.

Čo sa týka kategorických premenných, tam je to ešte komplikovanejšie. V procedúre je zatiaľ implementovaná možnosť pracovania s indikátormi ako s číselnými premennými a výpočet založený na rozdiele pravdepodobností počítaných z funkcie pravdepodobnosti, kde za nezávislé premenné sa dosadia ich priemerné hodnoty. Ak by však niekto potreboval prístup cez počítanie pravdepodobností pre jednotlivé kombinácie kategórií kategorických premenných, môže využiť priamo procedúru Generalized Linear Models v IBM SPSS Statistics. 

Rádi byste celé problematice porozuměli do hloubky? Ing. Mgr. Milan Machalec vám rád předá jeho cenné zkušenosti, které můžete získat prostřednictvím našich analytických a statistických kurzů. Navštivte naše kurzy, kde vám rádi pomůžeme při vašem růstu v oblasti statistiky a analýzy dat.