Analýza rozptylu a její předpoklady III

V minulých dvou článcích jsme se zabývali chováním testů pro shodu středních hodnot ve skupinách při platnosti nulové hypotézy a nesplnění předpokladů klasické analýzy rozptylu. Konkrétně jsme zkoumali klasický ANOVA test, robustní testy Welchův a Brownův-Forsytheův a neparametrický Kruskalův-Wallisův test. Nyní se zaměříme na vlastnosti testů, pokud platí alternativní hypotéza. Zkoumat budeme sílu testu, tedy pravděpodobnost, že test správně zamítne nulovou hypotézu a přijme alternativní. To ale výrazně závisí na míře, s jakou je nulová hypotéza ve skutečnosti porušena. Nezískáme tedy jedno číslo, ale celou funkci pro sílu testu, té se také někdy říká silofunkce. Míra porušení nulové hypotézy se definuje tzv. velikostí efektu, zkráceně ES (Effect Size). Čím větší hodnota, tím se situace více liší od nulové hypotézy.

Síla testu

ES je pro mnoho testů v podstatě testová statistika, ze které je odstraněn vliv počtu případů. U analýzy rozptylu je hodnota ještě odmocněna, druhá mocnina ES je rovna podílu vnitroskupinového (WSS) a meziskupinového (BSS) součtu čtverců. Jiné vyjádření velikosti efektu vychází z vysvětleného rozptylu, pak je velikost efektu rovna podílu vnitroskupinového a celkového součtu čtverců, podíl se nazývá η2. Mezi oběma formulacemi platí jednoduchý vztah.

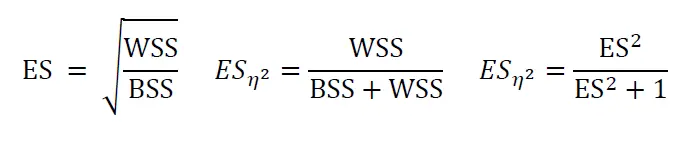
V simulaci se uvažovaly hodnoty ES od 0 do 0,55, podle druhého vyjádření do 0,23. Horní hranice je již považována za silný efekt. Simulace byly provedeny pro 50 různých hodnot ES a pro každou bylo vytvořeno 40 000 simulací, zvlášť pro každý test a odlišné parametry simulace. To umožnilo stanovit podrobně vývoj silofunkce jednotlivých testů. Silofunkce závisí také na zvolené hladině významnosti testu a počtu případů. První hodnota je standardních 5 % a druhá 60 případů ve výběru, jako při ověřování testů při platnosti nulové hypotézy.

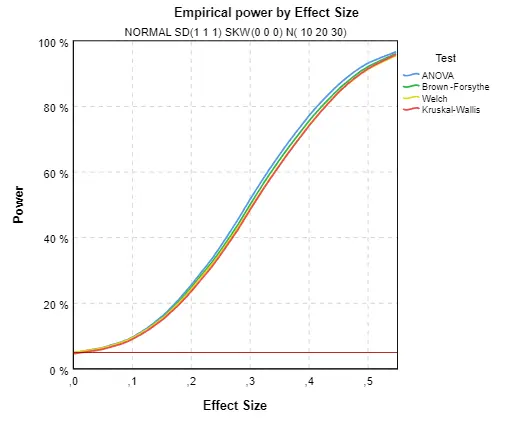
Silofunkce jsou různé pro každou kombinaci parametrů simulace a nelze je proto zde všechny uvést. Zaměříme se jen na reprezentanty typických situací. Na Obr. 1 je síla testu při splnění všech předpokladů testu ANOVA, graf zachycuje ideální situaci. Silofunkce v bodě 0 je vždy rovna empirické signifikanci. Pokud je ES rovna 0, jedná se vlastně o nulovou hypotézu a silofunkce má interpretaci empirické signifikance. Čím větší je ES, tím je silofunkce větší, protože nulová hypotéza je tím pravděpodobněji zamítnuta, čím více je porušena. Síla závisí také na počtu případů, proto je pro obecné závěry smysluplné jen porovnávat jednotlivé testy. Síla jednotlivých testů je při splnění předpokladů ANOVA téměř stejná, ale při podrobnějším pohledu si lze všimnout, že nejvyšší hodnoty dosahuje klasický test ANOVA. Hodnoty Silofunkcí v bodě 0 jsou 5 %, což odpovídá zjištěním v minulém článku Analýza rozptylu a její předpoklady II. V ideální situaci můžeme zvolit prakticky libovolný test. Srovnáním se situací, kdy jsou všechny skupiny navíc stejně veliké, bychom zjistili, že síla testu je stejná. Není tedy pravda, že síla testu je největší u stejně velkých skupin, jak se někdy traduje.

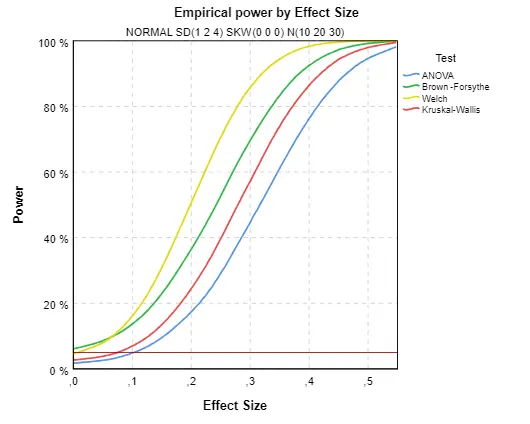
Na Obr. 2 je situace, kdy je výrazně porušena normalita, ale jsou zachovány stejné rozptyly ve skupinách. Data jsou sešikmena, přičemž je sešikmení ve všech skupinách stejné. V této situaci výrazně vyniká Kruskalův-Wallisův test. Taková data jsou pro jeho použití nejvhodnější, protože se srovnávají skupiny s nenormálním rozdělením, které se mezi sebou liší jen střední hodnotou, tvar rozdělení je stejný. Silofunkce v bodě 0 (signifikance) je u všech testů přibližně správných 5 %, což opět odpovídá závěrům z minulého článku.

Na Obr. 3 jsou silofunkce v situaci, kdy data mají normální rozdělení ve skupinách, ale rozptyly jsou různé. Z předchozích článků víme, že v této situaci je nutné použít robustní testy, aby byla signifikance spočtena správně. Vhodnost robustních testů dokládají i jejich silofunkce, které nejen začínají přibližně na správné hodnotě 5 %, ale nabývají i větších hodnot než u klasického testu ANOVA nebo neparametrického Kruskalova-Wallisova testu. Z robustních testů dosahuje lepších výsledků Welchův test.

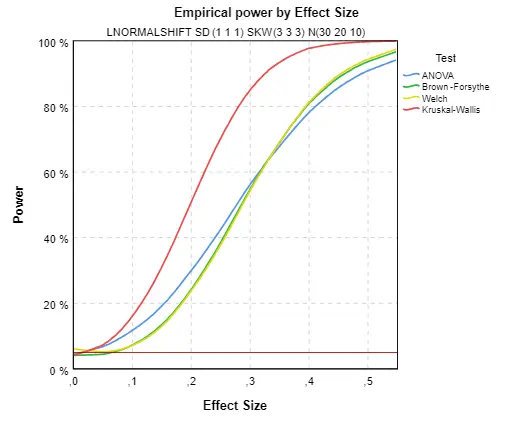
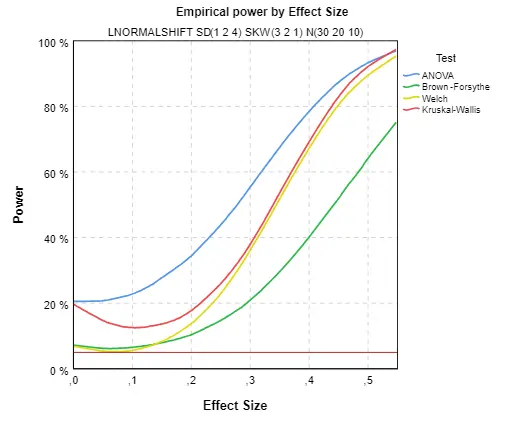
Obr. 4 ukazuje nejméně příznivou situaci, kdy data mají různé rozptyly ve skupinách a pocházejí z výrazně šikmého rozdělení. Z předchozího článku víme, že signifikanci nepočítá správně žádný test, ačkoliv robustní testy jsou jí nejblíže. Z grafu je patrné, že nejsilnějším testem je klasická ANOVA, to je však jen díky tomu, že začíná na signifikanci okolo 20 % a ne na 5 %, které by měla správně dosáhnout.  Protože nevíme, která hypotéza ve skutečnosti platí, je tento test v praxi nepoužitelný. Pokud by platila nulová hypotéza, byl by velmi zavádějící. Podobné je to s Kruskallovým-Wallisovým (KW) testem, signifikance opět neodpovídá 5 %. Test má i zvláštní průběh silofunkce, která nejprve klesá a teprve pak roste. Důvodem je odlišně formulovaná nulová hypotéza testu. Ta tvrdí, že skupiny pocházejí ze stejného rozdělení, rozdělení se mohou lišit i jinak než střední hodnotou, např. rozptylem nebo šikmostí. Náš efekt odráží odlišnost jen ve středních hodnotách a není to přesně ten efekt se kterým KW test počítá. Pro přesné chování KW testu by se musela použít specificky spočtená velikost efektu. Pokud nás zajímají jen střední hodnoty je v této situaci KW nejméně vhodnou variantou. Nejlepší možností zůstávají robustní testy. I ony mají skutečnou signifikanci odlišnou od 5 %, ale rozdíl je z uvažovaných testů nejmenší. Z průběhu silofunkce vychází jako nejlepší Welchův test. Malý pokles silofunkce je i u Brownova-Forsytheova testu, jeho nulová hypotéza je zde sice stejná jako u ANOVA, ale ES se počítá mírně odlišně, což vedlo k mírnému poklesu silofunkce.

Závěrem lze shrnout, že v případě splnění všech předpokladů pro ANOVA jsou testy téměř ekvivalentní. Při nesplnění se musíme nejprve řídit správností signifikance (viz Analýza rozptylu a její předpoklady I a II) a pak můžeme volit silnější test. Největší rozdíl v síle je při správném použití KW testu, tedy pro situaci, kdy rozdělení nejsou normální, ale jejich tvar je ve skupinách shodný a liší se jen posunutím. Pak je KW test silnější než klasická ANOVA nebo robustní testy.

Rádi byste se o statistice a analýze dat dozvěděli více? Chcete se stát mistrem ve svém oboru nebo si jen potřebujete doplnit znalosti? V ACREA nabízíme širokou nabídku kurzů pro váš profesní růst. Máte-li jiný dotaz. Nebojte se využít naši nezávaznou konzultaci, při které vám rádi zodpovíme všechny vaše dotazy a najdeme vhodné řešení.