T-testy: Klíč k odhalení rozdílů mezi skupinami

Statistika nabízí celou řadu metod, jak ověřit naše hypotézy a rozhodnout, zda rozdíly mezi skupinami či měřeními mají skutečný význam. Jednou z nejčastěji používaných metod je t-test, který se uplatňuje v přírodních vědách, medicíně, vzdělávání, průmyslu i v sociálních vědách. Tento článek se zaměřuje na vysvětlení, co t-test je, jaké existují jeho druhy, jak se počítá a kde se s ním můžeme setkat v praxi.
Co je t-test?
T-test je statistická metoda určená k testování hypotézy o středních hodnotách. Jinými slovy ověřuje, zda rozdíl mezi dvěma průměry, kterými střední hodnoty odhadujeme, je dostatečně velký na to, abychom jej mohli považovat za statisticky významný, nebo zda by mohl vzniknout čistě náhodou.
V jádru stojí otázka: „Je rozdíl, který pozoruji, skutečný, nebo je to jen variabilita v datech?“ T-test využívá t-rozdělení (Studentovo rozdělení), které na malých souborech test vyžaduje, aby data pocházela z normálního rozdělení. Od velikosti souboru 30-ti případů už ale předpoklad normality není nutný.
Druhy t-testů a jejich využití
Existuje několik variant t-testů, které se liší podle situace, ve které jsou aplikovány. Nejčastější jsou následující:
- Jednovýběrový t-test
Tento test porovnává průměr výběru s nějakou známou nebo očekávanou hodnotou.- Praktický příklad: Chceme zjistit, zda očekávaná (střední) hodnota výšky rostliny v experimentu je skutečně 20 cm. Vytvoříme náhodný výběr 30 rostlin, vypočítáme průměr a porovnáme jej s hodnotou 20 pomocí t-testu.
- Nezávislý dvouvýběrový t-test
Slouží k porovnání průměrů dvou nezávislých skupin.- Praktický příklad: Máme dvě skupiny studentů – jedna absolvovala klasickou výuku a druhá nový výukový program. Chceme zjistit, zda se očekávaná hodnota skóre testů těchto dvou skupin významně liší.
- Párový t-test
Používá se tehdy, když máme dvojici měření u stejného objektu či osoby.- Praktický příklad: U studentů změříme skóre testu před školením a po něm. Porovnáváme tedy výsledky „před a po“ u stejné skupiny, čímž eliminujeme vliv individuálních rozdílů.
Jak se t-test počítá?
Výpočet t-testu se odvíjí od základního principu: rozdíl mezi průměry se porovnává s variabilitou dat. Čím větší je rozdíl vzhledem k variabilitě, tím vyšší je hodnota testové statistiky t.
Obecný postup výpočtu:
- Stanovíme nulovou hypotézu (např. „rozdíl mezi skupinami není“).
- Vypočítáme průměry a směrodatné odchylky příslušných skupin ve výběru.
- Na základě velikosti výběru a rozptylu určíme hodnotu t-statistiky.
- Pomocí t-rozdělení a počtu stupňů volnosti zjistíme p-hodnotu.
- Porovnáme p-hodnotu s hladinou významnosti (typicky 0,05).
- Pokud je p < 0,05, zamítáme nulovou hypotézu a rozdíl považujeme za statisticky významný.
Příklad:
U skupiny studentů zjistíme průměrné zlepšení skóre po školení o 5 bodů. Párový t-test spočítá, zda je toto zlepšení statisticky významné, nebo zda by mohlo být výsledkem náhody. Pokud je výsledek p-hodnoty 0,01, znamená to, že pravděpodobnost náhodného vzniku takového rozdílu je jen 1 %.
Metody a nástroje pro výpočet t-testu
Dávno již není nutné počítat t-test ručně, ale existuje celá řada softwarových nástrojů a programovacích jazyků, které tento výpočet zvládnou během okamžiku. Mezi analytiky nejpoužívanější patří:
- IBM SPSS Statistics – statistický software vhodný pro uživatele, kteří preferují klikací rozhraní před programováním.
- R a Python – programovací jazyky oblíbené v datové analýze, které umožňují výpočty t-testů i rozsáhlé statistické modelování.
- Microsoft Excel – nabízí funkce, které umožní provést t-test přímo nad tabulkami.
Použití softwaru zároveň usnadňuje interpretaci výsledků – typicky dostaneme tabulku s hodnotou t-statistiky, stupni volnosti a p-hodnotou.
Ukázka výpočtu párového t-testu v IBM SPSS Statistics
Výpočet párového t-testu si ukážeme na datovém souboru, kde lékaři testovali účinky nového typu diety pro pacienty se sklonem k srdečním chorobám. Datový soubor obsahuje informace o 59 pacientech, u nichž byla po dobu šesti měsíců tato dieta aplikována. U každého pacienta byla zaznamenána hmotnost před začátkem diety a po jejím ukončení.
Volání procedury v IBM SPSS Statistics
Analyze → Compare Means → Paired-Samples T Test
Nastavení dialogu
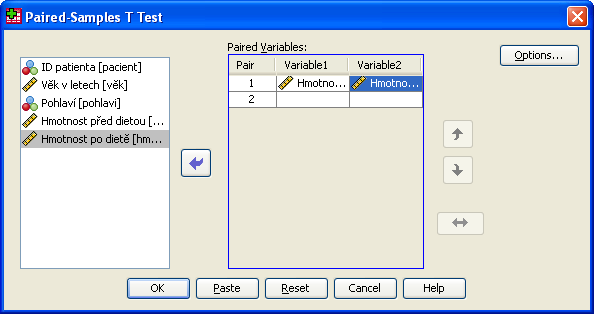
Do pole Paired Variables přeneseme dvojici proměnných, jejichž střední hodnoty porovnáváme. Pokud zadáme dvojic více, provede se pro každou z nich test samostatně.
Tlačítko Options
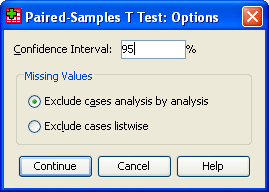
V poli Confidence Interval zadáme požadovanou hladinu spolehlivosti (pro výpočet intervalu spolehlivosti rozdílu průměrů).
Přepínačem Missing Values řídíme způsob zacházení s chybějícími hodnotami. Je-li třeba vyloučit z analýzy všechny případy, které obsahují u některé z testovaných proměnných vynechanou hodnotu, zvolíme Exclude cases listwise. Chceme-li u každé proměnné samostatně využít maximální možný počet případů, označíme Exclude cases analysis by analysis.
Výstupy
Tabulka popisných statistik párových proměnných
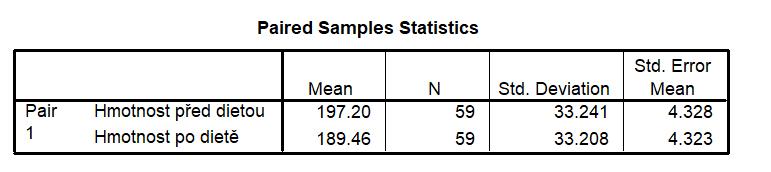
Tabulka Paired Samples Statistics obsahuje pro obě proměnné přehled těchto popisných statistik: počet případů (N), průměr (Mean), směrodatná odchylka (Std. Deviation) a standardní chyba průměru (Std. Error Mean). Průměrná hmotnost pacientů před začátkem diety byla 197 kg na konci diety 189 kg.
Korelace párových proměnných
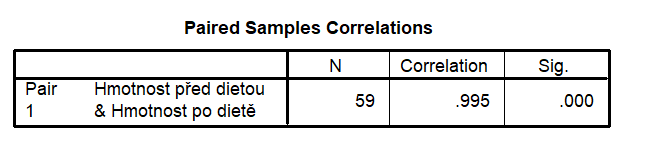
V tabulce je zobrazen počet případů (N), Pearsonův lineární korelační koeficient (Correlation) a hodnota signifikance (p-hodnota) pro nulovou hypotézu o nulovosti korelačního koeficientu (Sig). Z tabulky vyplývá, že sledované proměnné jsou na sobě velmi silně závislé – korelační koeficient se blíží jedné. Rovněž nízká hodnota signifikance vyjadřuje, že je třeba nulovou hypotézu zamítnout (tj. korelační koeficient není roven nule).
Výstupní tabulka párového T-testu

Pomocí výstupní tabulky párového T-testu rozhodujeme o tom, zda zamítneme nebo nezamítněme nulovou hypotézu o shodě středních hodnot. V našem případě je nulová hypotéza formulována tak, že střední hodnota hmotnosti pacienta před začátkem diety je stejná jako střední hodnota hmotnosti po ukončení diety.
Ve sloupcích postupně čteme: průměrný rozdíl sledovaných proměnných (Mean), směrodatnou odchylku rozdílu (Std. Deviation), standardní chybu průměru pro rozdíl (Std. Error Mean), dolní a horní mez intervalu spolehlivosti pro rozdíl (Confidence Interval of the Difference), hodnotu Studentovy statistiky t (t), počet stupňů volnosti (df) a significance při oboustranné alternativní hypotéze (Sig. (2-tailed)).
Počet stupňů volnosti je nutný k přesnému určení Studentova t rozložení. Na základě significance potom rozhodujeme, zda zamítneme nebo nezamítneme nulovou hypotézu na předem zvolené hladině spolehlivosti (na 95% hladině spolehlivosti zamítáme nulovou hypotézu v případě, že je hodnota significance < 0,05).
V našem případě je průměrný úbytek na váze po aplikaci diety 7,746 kg. Interval spolehlivosti napovídá, že nulovou hypotézu T-testu je třeba zamítnout, protože nula neleží uvnitř intervalu. Rovněž nízká hodnota significance vyjadřuje, že rozdíl v hmotnosti pacienta před začátkem diety a po jejím ukončení je statisticky významný.
K čemu t-testy slouží?
T-testy jsou praktickým nástrojem tam, kde potřebujeme ověřit, zda pozorovaný rozdíl má smysl. Využívají se například:
- Ve výzkumu a vědě – testování účinnosti léčiv, porovnávání experimentálních a kontrolních skupin.
- Ve vzdělávání – ověřování, zda nová metoda výuky přináší lepší výsledky.
- V průmyslu – porovnávání výrobních procesů, kontrola kvality.
- V marketingu a sociálních vědách – zkoumání vlivu reklamních kampaní, rozdílů mezi skupinami zákazníků.
T-testy představují základní, a přitom nesmírně užitečný statistický nástroj. Umožňují nám odlišit skutečné rozdíly od náhodného kolísání dat. Ať už pracujete v akademickém výzkumu, zdravotnictví, průmyslu nebo obchodu, znalost principů t-testu vám poskytne silný argument při interpretaci výsledků. Díky dostupným softwarovým nástrojům navíc není složité t-testy počítat a využívat je ve své praxi.
Rádi byste se o statistice a analýze dat dozvěděli více? Chcete se stát mistrem ve svém oboru nebo si jen potřebujete doplnit znalosti? V ACREA nabízíme širokou nabídku kurzů pro váš profesní růst. Máte-li jiný dotaz. Nebojte se využít naši nezávaznou konzultaci, při které vám rádi zodpovíme všechny vaše dotazy a najdeme vhodné řešení.





