Lze odhadnout smrtnost koronaviru během trvání pandemie?
Smrtnost koronaviru spočteme jako počet zemřelých na koronavirus děleno počet nakažených. Počty nakažených, počty mrtvých i počty uzdravených se mění každý den. Většina nakažených se doposud neuzdravila ani nezemřela. Lze v takové situaci odhadnout smrtnost koronaviru, nebo musíme počkat, až pandemie skončí?
Zpočátku to vypadalo, že se koronavirem nakazíme téměř všichni a budeme se jen snažit šíření nemoci zpomalit, aby nedocházelo k zahlcení našeho zdravotnictví a ke zbytečným úmrtím. Od začátku si proto kladu otázku: Jaká je pravděpodobnost, že nakažený jedinec na koronavirus zemře? Sleduji jako mnozí z nás denní počty pozitivních případů, úmrtí a zotavení a snažím se z nich odhadnout celkovou smrtnost koronavirové pandemie.
Data, která máme k dispozici jsou zatížena nepřesnostmi. S tím bohužel nemůžeme nic dělat, ale považuji za vhodné ty hlavní připomenout:
- Počet nakažených je zřejmě větší než počet jedinců s pozitivními testy. Podíl nakažených s latentními příznaky by bylo možné zjistit pouze reprezentativním výzkumem. Dále v textu bude počet nakažených ve skutečnosti znamenat počet pozitivně testovaných.
- Počet pozitivních výsledků testu ovlivňuje počet provedených testů. Korelace mezi počtem testů a počtem pozitivních výsledků je 0,8.
- Na koronavirus umírají především lidé s podlomeným zdravím a často nelze s jistotou říci, že primární příčinou jejich úmrtí byl koronavirus či jiná nemoc.
- Denní počty uzdravených ovlivňuje metodika prokazování uzdravení.
- Stále není známo, jak dlouho je zotavený jedinec imunní. V počtech pozitivních se proto mohou vyskytovat duplicity.
- Data o počtu mrtvých a uzdravených se zpětně korigují. Není výjimkou, že se změní počty mrtvých dva týdny staré, počty uzdravených se významně změnily i s více než měsíčním zpožděním.
- Data nejsou snadno dostupná. Zpočátku se na stránkách Ministerstva zdravotnictví zveřejňovaly pouze denní kumulace, až v posledních dnech jsou k dispozici denní počty mrtvých a zotavených. Ostatní podrobnější zdroje se od MZČR odchylují.
Denní počty případů zatížené uvedenými nepřesnostmi znázorňuje následující graf.
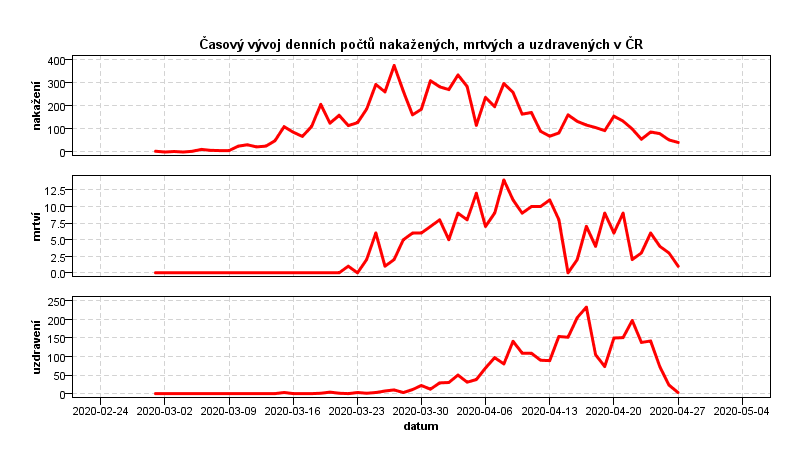
Ačkoli časové řady fluktuují, z grafu je zřejmé, že počet denních přírůstků nakažených již několik týdnů klesá. V současnosti je již nárůst zotavených větší než nárůst nakažených a pandemie ustupuje. V grafu si dále můžeme povšimnout, že denní počty mrtvých pravděpodobně také překonaly své maximum. Denní počty zotavených možná stále rostou, propad na konci grafu zmizí po zpětné aktualizaci dat. Z pozorování trendů lze usoudit, že doba od nákazy do smrti je kratší než doba od nákazy do zotavení.
Pokud bychom chtěli modelovat vývoj počtů nakažených jedinců v populaci, je na místě použít některý ze známých epidemiologických modelů, nejznámější z nich je model SIR. V médiích často prezentovaný reprodukční poměr udávající průměrný počet nakažení zdravých jedinců od jednoho nemocného hraje při epidemiologické modelování klíčovou roli. Epidemiologové mají k dispozici i model SIRD, kde na rozdíl od SIR se jedinci s ukončenou chorobou rozdělují mezi mrtvé i imunní. Pravděpodobnost úmrtí, která by se z odhadnutého modelu SIRD dala určit, se však mediálně neprezentuje, proto jsem se rozhodl udělat si vlastní, jednodušší statistický model, jehož parametrem je přímo smrtnost.
V mém jednoduchém modelu každý nakažený zemře s konstantní pravděpodobností p (smrtnost) a s pravděpodobností 1-p se zotaví. Dostupná data bohužel přímo neříkají, kolik z nakažených konkrétní den někdy v budoucnu zemřelo, resp. se zotavilo. Máme k dispozici pouze denní počty mrtvých a zotavených, kteří se mohli nakazit kterýkoli den před úmrtím či zotavením. Proto jsem musel model rozšířit a modelovat i dobu od nakažení do úmrtí pro ty, kteří zemřou, a dobu od nakažení do zotavení pro ty, kteří se zotaví.
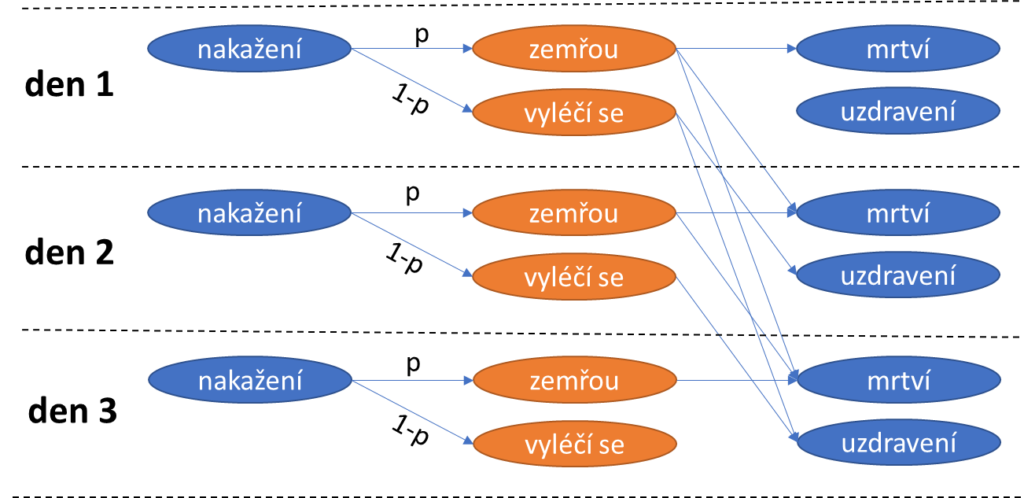
Nakažený jedinec zemře s pravděpodobností p, k úmrtí může dojít v den nákazy nebo v jakýkoli následující den. Nakažený jedinec se zotaví s pravděpodobností 1-p, k zotavení může dojít v jakýkoli den následující po nakažení. Pozorujeme jen modré denní počty nakažených, mrtvých a uzdravených.
Rozdělení mezi mrtvé a zotavené jsem modeloval pomocí binomického rozdělení, doby do úmrtí a do zotavení v modelu popisují multinomická rozdělení. Nejprve jsem se snažil metodou maximální věrohodnosti odhadnout všechny neznámé pravděpodobnosti v rozděleních, ale ukázalo se, že již samotný výpočet věrohodnosti je příliš komplikovaný. Z toho důvodu jsem se omezil pouze na modelování očekávaných denních počtů mrtvých a zotavených.
V rovnicích sestavených pro očekávané počty se objeví všechny potřebné pravděpodobnosti včetně smrtnosti. Sestavené rovnice by se daly řešit pomocí běžné lineární regrese bez konstantního členu, avšak abych zajistil, že odhadované parametry budou skutečně pravděpodobnosti z intervalu mezi nulou a 100 %, musel jsem řešit nelineární soustavu rovnic s okrajovými podmínkami.
Model jsem nejdříve testoval na simulovaných datech se známou smrtností. Pak jsem začal sbírat reálná data. První registrované případy se v ČR objevily 1.března 2020, a tak máme nyní na konci dubna k dispozici časové řady s více než padesáti pozorováními. Odhady jsem začal počítat v první polovině dubna, dříve byly časové řady příliš krátké vzhledem k počtu parametrů modelu.
Díky fluktuacím v malých počtech jsem musel ještě několik dní vyčkat, než se odhady ustálí. Jak jsem si experimentálně ověřil na simulovaných datech i na datech z jiných zemí, pokud modelem provádíme odhady příliš brzy, kdy jsou časové řady krátké a pozorujeme spíše úmrtí než zotavení, model smrtnost nadhodnocuje. V ČR například v prvním dubnovém týdnu model odhadoval smrtnost okolo 6 %, avšak během času tato odhadovaná hodnota klesala. Dnes model odhaduje smrtnost v ČR na hladině 3,2 % a pokles nepozoruji.
A jak to vypadá v jiných zemích? Model jsem nejprve ověřil na Číně, kde pandemie už pominula a smrtnost ve výši 4 % je známá. Nejlépe jsou na tom zatím na Slovensku. Tam většina denních počtů úmrtí je nulová a modelem proto nelze smrtnost uspokojivě odhadnout, resp. model zatím predikuje téměř nulovou hodnotu. Naopak velmi vysokou smrtnost mají v Itálii, modelový odhad je ve výši 14 %. Některým zemím model sice odhaduje ještě vyšší smrtnost, ale jedná se o země, kde odhady ještě nejsou ustálené a klesají. Konkrétně mám na mysli Franci a Velkou Británii. Odhad se naopak již stabilizoval pro Španělsko na hodnotě 10 % a u Švýcarska na 3 %. USA mají v absolutním počtu ze všech zemí nejvíce mrtvých a pandemie je zasáhla poměrně pozdě. Odhady ještě nejsou stabilizované a klesají, smrtnost v USA jistě nepřesáhne 7 %.
Kromě smrtnosti jednoduchý statistický model umožnil i odhadnout pravděpodobnosti, za kolik dní po nákaze jedinec zemře, resp. se uzdraví. V České republice k úmrtí dojde nejpravděpodobněji mezi devátým a jedenáctým dnem od nákazy. Zotavení trvá déle, po poslední významné zpětné aktualizaci dat o zotavených se zotavení začala kumulovat do dob tři týdny a pět týdnů, což zřejmě souvisí s metodikou prokazování uzdravení.
Zajímavé zjištění o době od nákazy do úmrtí poskytl model pro Čínu. Čtvrtina mrtvých tam zemřela ve stejný den, jako se nakazila. To ukazuje na nedostačující testování živých jedinců. U mnoha nakažených Číňanů byl koronavirus diagnostikován až po smrti.





Vdaka Ondro, pekny zrozumitelny clanok, potesil si ma.
Vsetko dobre, vela zdravia, ked prides na Slovensko do Bratislavy ozvi sa rada sa s Tebou stretnem Olga
Jenom malá terminologická poznámka. Bylo by přesnější odlišovat okamžik diagnostikování nemoci a okamžik nakažení se. Pacienti pravděpodobně většinou neumírali ve stejný den, kdy se nakazili, ale zejména v počátcích epidemie v Číně bylo asi časté, že nemoc byla diagnostikována až v okamžiku, kdy k nemocného přivolali lékaře až v terminální fázi onemocnění.
Nejspíš i ten model funguje lépe, pokud se jako počátek onemocnění bere okamžik diagnózy, jednak přesnější údaj nemáme a jednak tím odpadá možné zkreslení dané tím, že krize u Covid-19 často přichází až po přechodném zlepšení zhruba týden po prvních vážnějších příznacích.
Jinak pěkný článek a i ten odhad smrtnosti mi přijde dosti pravděpodobný. Když jsem se to pokoušel počítat já, porovnával jsem počty uzdravených s počty úmrtí – 7. To proto, že pokud u pacienta vymizí příznaky, musí projít dvěma negativními testy s odstupem 5 dní, což jsem při připočtení doby na vyhodnocení testu zaokrouhlil na týden.
Zkoušel jsi ten model přepočítat za předpokladu, že asymptomatických nákaz může být x-krát víc, než evidovaných pacientů?
Kolik to x může být naznačily rakouské testy, kde jim to počátkem dubna vycházelo na cca x=3. Kolik to může být u nás se snad dozvíme na tiskové konferenci zítra.
V popisu modelu používám okamžik nakažení, ale mám ve skutečnosti na mysli okamžik pozitivní diagnózy, jak jsem napsal v první odrážce v úvodu článku. Těchto datových nepřesností je celá řada, možná by se našla ještě další nepřesnost, kterou jsem opomněl. Ty hlavní se mi snad podařilo v úvodu vyjmenovat.
Neznámým okamžikem nakažení je bohužel zkreslena i doba do úmrtí, ve skutečnosti se jedná o dobu od pozitivní diagnózy do úmrtí. Ještě více je zkreslena doba do uzdravení. Jak popisujete, okamžik uzdravení je zkreslen opakováním testu a dobou vyhodnocení. Proto v modelu se nevyskytuje doba od nákazy do uzdravení, ale doba od pozitivního vyhodnocení úvodního testu do negativního vyhodnocení následného negativního testu.
Navíc vykazování má zpoždění někdy i v řádu týdnů, takže se nelze spolehnout ani na statistiky mrtvých.
Model jsem nezkoušel modifikovat pro nakažené s latentními příznaky. Pro odhad celkové smrtnosti je však ani nemusím zanášet do modelu. Předpokládáme-li, že latentní nákaza končí vždy uzdravením a známe odhad smrtnosti pozitivně diagnostikovaných z modelu, je celková smrtnost rovna smrtnosti pozitivně diagnostikovaných krát 1/x, kde x vyjadřuje kolikrát je větší počet všech nakažených než pozitivně diagnostikovaných.
Děkuji moc za komentáře, opět jsem si ověřil, že je zbytečné budovat sofistikované modely, pokud nemáme reliabilní data.
Díky, vážený pane doktore! Rozhodně poučné! To, že jsem napsal „líbí se“ nemá s estetikou nebo pocity při tení nic společného. Je to zkrátka vědecky zajímavé. Patřím do skupiny lidí, kteří bývají označováni jako „vulnerable“, zranitelní. Když se podívám jen na přehled počtu zemřených podle věku, napadá mi, že se smrtnost může dost významně lišit třeba podle věkových skupin. Bohužel nebývají uveřejňována data o věku nakažených osob, jen o věku zemřelých. Dalo by se aspoň zhruba odhadovat smrtnost pro jednotlivé věkové skupiny lidí?
To by asi ale cenzura nepustila do médií. Přitom bychom (samozřejmě bohužel) nebrali v úvahu chronické nemoci.
Srdečně
Hynek Jeřábek
Otázka vztahu smrtnosti a věku je plně na místě. A dále se můžeme ptát, jak se smrtnost liší podle pohlaví, regionu, zaměstnání, zdravotního stavu atd. Model, který by toto odhalil, bychom museli postavit nad individuálními daty. Správně píšete, že taková data jsou k dispozici jen pro zemřelé, a musím dodat, že ještě v dosti omezené míře. To je pro sestavení modelu nedostatečné. Model, který popisuji v příspěvku, jsem vybudoval s ohledem na dostupná data. Předpokládám v něm, že pravděpodobnost úmrtí na koronavirus je u každého nakaženého stejná. To zřejmě pravda není. I přesto, že jde o zjednodušený model, potýkal jsem se při jeho odhadování s kvalitou dostupných dat. Úmrtí i uzdravení se zpětně upravují, například dnes jsem zkusil znovu spočíst odhady nad aktuálními daty a zjistil jsem, že se změnili počty od poloviny března! Odhad smrnosti v ČR mi dnes vyšel 3.3 %.
Dnes začínají vycházet první komentáře k plošné studii promoření. To je sice jiný pohled na věc, ale její zpracovatelé zajisté mají individuální data, takže bychom se mohli dovědět, jak je to s promořením různých věkových skupin. A pokud by zpracovatelé získali v budoucnu i data o umírání účastníků studie, mohli by nabídnout i tu smrtnost v závislosti na věku.