Korelace – co jste o nich věděli i nevěděli

Analýza vztahů v datech patří k základním úlohám statistiky. Snad každý analytik si někdy položil otázku, jak silný je vztah mezi dvěma proměnnými, zda může jedna veličina vysvětlovat chování jiné, nebo jak moc společné informace v sobě nesou dvě proměnné. Odpověď na tyto otázky, především pro číselné proměnné, hledá korelační analýza. Ačkoliv jsou její základní myšlenky poměrně běžně známé, v praxi se jejich aplikace často omezuje pouze na rutinní užití Pearsonova lineárního korelačního koeficientu. Korelační analýza však nabízí i mnoho dalších možností. V tomto článku si shrneme známé i některé méně známé informace o korelacích, představíme si i jiné typy korelačních koeficientů a rovněž si přiblížíme historické souvislosti vzniku těchto metod.

Historie

Historicky spadá hlavní zájem o tuto problematiku do poslední čtvrtiny 19. století a první čtvrtiny 20. století. Otázkou vztahů v datech se však zabývali již dříve například Pierre-Simon Laplace (1749 – 1827) nebo Carl Fridrich Gauss (1777 – 1855). Během tohoto období dochází k rychlému rozvoji oborů jako například biometrika, které vyžadují vývoj nové metodologie. Hlavní myšlenky a nástroje korelační analýzy byly vyvinuty právě v souvislosti s praktickými potřebami těchto oborů. Pojem korelace navrhl Francis Galton (1822 – 1911), bratranec Charlese Darwina a všestranný vědec, který se mimo jiné věnoval otázkám genetického výzkumu, dědičnosti a prokázání Darwinovy teorie, objevil možnost využití otisků prstů, zavedl pojem regrese k průměru, založil časopis Biometrika a biometrickou laboratoř. Matematický rámec metodologie tak, jak ho známe dodnes, poskytl Galtonův blízký spolupracovník Karl Pearson (1857 – 1936), matematik, filozof, zakladatel matematické statistiky a biometrie a dlouholetý redaktor časopisu Biometrika. Mezi těmi, kteří později významně přispěli k vytvoření přesné teorie, je třeba zmínit také Ronalda Aylmera Fishera (1890-1962), který je považován za zakladatele moderní statistiky. První komplexní aplikaci této metodologie, tzv. metodu dráhových koeficientů (path analysis), navrhl americký genetik Sewal Wright (1889- 1988).

Pearsonův lineární korelační koeficient

Pojem korelace vychází z latinského výrazu correlatio, který vyjadřuje vzájemný vztah. Korelace zkoumá společnou variabilitu dvou veličin a zjišťuje, zda můžeme v datech sledovat tzv. souběžnost, kdy se s vyššími hodnotami jedné proměnné pojí vyšší hodnoty druhé proměnné, nebo naopak tzv. protiběžnost, kdy vyšším hodnotám jedné proměnné odpovídají nižší hodnoty druhé. K tomuto účelu se zavádí pojem kovariance, která měří sílu lineárního vztahu mezi dvěma proměnnými – kladné hodnoty ukazují na souběžnost v datech, záporné na protiběžnost a hodnoty blízké nule na nedostatek lineárního vztahu. Z hlediska interpretace však tato charakteristika není příliš vhodná, protože její absolutní hodnota závisí na variabilitě proměnných a pouze na základě její velikosti tedy nelze usuzovat o síle vztahu. Proto se kovariance standardizuje vzhledem k rozptylům proměnných a tímto způsobem se zavádí nejznámější korelační koeficient, tzv. Pearsonův lineární korelační koeficient.

Pearsonův lineární korelační koeficient r vyjadřuje míru lineárního vztahu mezi dvěma číselnými proměnnými. Jeho hodnoty leží v intervalu <-1,1>, což výrazně usnadňuje interpretaci. Mezi jeho základní vlastnosti patří:

• korelační koeficient je definován, pokud jsou k dispozici alespoň dvě pozorování (pro praktické užití je však vhodné, aby bylo pozorování více) a obě proměnné mají nenulovou variabilitu,
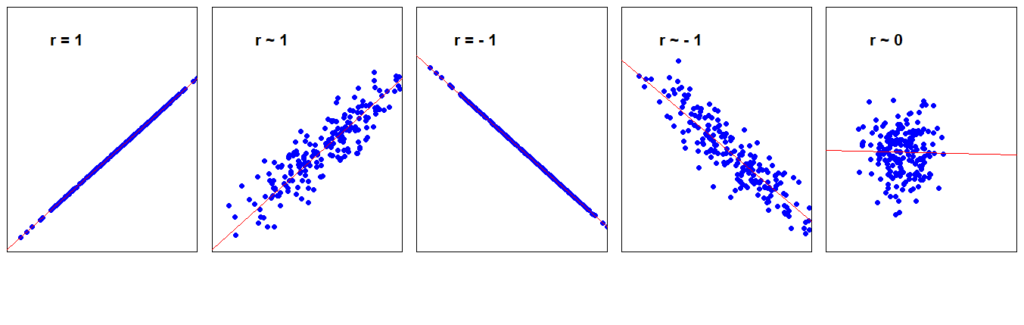
• r = 1 právě tehdy, když všechny body leží na přímce s kladnou směrnicí (přímka je rostoucí),  
• r = -1 právě tehdy, když všechny body leží na přímce se zápornou směrnicí (přímka je klesající),
• čím více se r blíží jedné, tím více se body shlukují kolem stoupající přímky; čím více se r blíží k mínus jedné, tím více se body shlukují kolem klesající přímky,
• jestliže v mraku bodů nelze vystopovat žádný lineární trend, je r = 0,
• korelační koeficient je symetrický, tj. r(X,Y) = r(Y,X),
• korelační koeficient se nezmění, pokud se škála jedné nebo obou proměnných posune o libovolnou konstantu, (změna měřítka).

Druhá mocnina korelačního koeficientu se označuje jako koeficient determinace. Uvádí se obvykle v procentech a vyjadřuje procento společné variability proměnných.

Při práci s korelacemi je třeba opatrnost s ohledem na možné zkreslení korelačního koeficientu. Nejčastějším typem problémů jsou extrémní hodnoty nebo šikmé rozložení dat. V takových případech je třeba zvážit vyloučení problematických případů, transformaci proměnných nebo užití neparametrických korelačních koeficientů. Normální rozložení dat není pro Pearsonův korelační koeficient nutnou podmínkou, představuje však výhodu vzhledem k absenci výše uvedených komplikací. Také v případě, že je mezi proměnnými nelineární vztah, není tento typ koeficientu vhodný. Z těchto důvodů je užitečné data nejprve prozkoumat graficky – jednak každou proměnnou samostatně pomocí histogramu nebo boxplotu a potom společně pomocí bodového grafu.

Pokud data představují výběr ze základního souboru, bývá zvykem rovněž testovat nulovost korelačního koeficientu. Při interpretaci výsledků je však třeba opatrnost, protože výsledek každého statistického testu závisí také na počtu pozorování. V případě malého datového souboru tak snadno vycházejí i zajímavé hodnoty korelačního koeficientu jako statisticky nevýznamné, v případě velkého souboru naopak i velmi slabé korelace jako statisticky významně odlišné od nuly. Vždy je tedy nutné vycházet také z absolutní hodnoty koeficientu. To, zda je hodnota korelačního koeficientu věcně zajímavá, záleží především na řešené úloze a rozhodnutí analytika. Existují však různá orientační doporučení, která se obvykle shodují na tom, že korelace v absolutní hodnotě menší než 0.3 mají jen minimální význam. Dále lze korelace rozdělit na základě absolutní hodnoty například do intervalů 0.3 – 0.5, 0.5 – 0.7, 0.7 – 0.9 a nad 0.9 s rostoucím významem pro interpretaci vztahu.

Pro více proměnných se hodnoty korelačních koeficientů obvykle tabelují do tzv. korelační matice, což je typicky čtvercová tabulka, která obsahuje korelační koeficienty pro všechny dvojice proměnných. Hodnoty na diagonále jsou rovny jedné a tabulka je symetrická podle diagonály, což vyplývá ze symetrie korelačního koeficientu.

Ačkoliv je Pearsonův lineární korelační koeficient primárně určený pro analýzu vztahů mezi číselnými proměnnými, lze ho rovněž užít pro dichotomické proměnné jako vyjádření korelace mezi dvěma jevy.

Neparametrické korelace

Jestliže užití Pearsonova lineárního korelačního koeficientu není vhodné například z důvodu výskytu extrémních hodnot nebo šikmého rozložení dat, představují alternativu tzv. neparametrické korelační koeficienty. Pravděpodobně nejznámější z nich jsou Spearmanovo ρ a Kendallovo τ.Tyto koeficienty vycházejí při výpočtu z pořadí a vzájemných pozic hodnot, proto nejsou citlivé na vzdálená pozorování. Neměří linearitu, ale shodu pořadí dvou statistických řad. Důvodem pro jejich užití může být rovněž nelineární vztah mezi proměnnými (především některé typy nelinearity), zvyklosti v oboru nebo potřeba porovnat výsledky s jinými výzkumy.

Spearmanovo ρ (rho) vnikne tak, že se do vzorce pro Pearsonův lineární korelační koeficient dosadí místo původních hodnot jejich pořadí. Kendallovo τ (tau) je založené na počtu souhlasných a nesouhlasných dvojic případů, kde souhlasné případy jsou takové, které lze spojit rostoucí úsečkou, nesouhlasné klesající úsečkou. Oba tyto koeficienty leží rovněž v intervalu <-1,1>, přitom 1 odpovídá plné shodě pořadí, –1 zcela protichůdným pořadím a 0 charakterizuje situaci, kdy mezi pořadími není žádný vztah.

Polychorické a polyseriální korelace

V některých oborech, zvláště v psychologii a jiných sociálních vědách, jsou oblíbené polychorické a polyseriální korelace. Ty nacházejí uplatnění například tam, kde se pracuje s dotazníky, v nichž respondenti hodnotí na určité škále. Polychorické a polyseriální korelace vyjadřují míru asociace mezi dvěma proměnnými v případě, že jedna nebo obě proměnné jsou ordinální kategorizované, avšak předpokládá se, že vznikly kategorizací určité latentní proměnné s normálním rozložením. S touto myšlenkou přišel již Karl Pearson, který si všiml, že je někdy obtížné určit přesnou hodnotu spojité veličiny jako je například barva očí a mnohem snazší je zařadit pozorování do uspořádaných kategorií. Otázkou však je, jak potom přiřadit každé kategorii číselnou hodnotu tak, aby zůstaly zachovány původní vztahy. Předpokládal tedy, že tyto kategorizované proměnné jsou funkcí určité číselné proměnné s přibližně normálním rozdělením a usiloval o odhad korelace mezi těmito latentními proměnnými.

Polychorické korelace představují způsob, jak odhadnout korelaci mezi dvěma latentními proměnnými s dvourozměrným normálním rozložením na základě dvou ordinálních proměnných, o nichž se předpokládá, že vznikly jejich kategorizací. Speciálním případem jsou tetrachorické korelace určené pro situaci, kdy jsou obě proměnné dichotomické.

Polyseriální korelace odhaduje latentní korelaci mezi číselnou proměnnou se spojitým rozložením a ordinální proměnnou, u které se předpokládá, že vznikla kategorizací číselné proměnné s normálním rozložením. Speciálním případem je biseriální korelace, která měří lineární závislost mezi spojitou číselnou a dichotomickou proměnnou, u které se rovněž předpokládá vznik na základě kategorizace normálně rozložené číselné proměnné.

Ačkoliv je pojem korelace často považován za synonymum analýzy vztahů v datech, neodpovídá to zcela skutečnosti. Korelace není jedinou možností, jak analyzovat vztah mezi dvěma proměnnými a záleží také na typech proměnných. Zatímco pro číselné proměnné se obvykle jedná o první volbu, například pro zkoumání vztahu mezi dvěma nominálními proměnnými je třeba užít kontingenční tabulku a míry asociace. Pro analýzu vztahu mezi číselnou proměnnou a určitým kategorizovaným faktorem se velmi dobře hodí analýza rozptylu.

Jak interpretovat korelace

Korelační analýza a na ni navazující metody mohou pomoci odhalit strukturu vztahů v datech. Při interpretaci výsledků je však třeba opatrnost. Korelace zjišťuje, zda v datech existuje souběh nebo protiběh variabilit dvou proměnných, neříká však nic o významu takového zjištění. Na výzkumníkovi potom je pokusit se interpretovat tyto vztahy také na základě znalosti problému. Korelace přitom nemusí nutně znamenat kauzální vztah, může se jednat například o dvě proměnné, které v sobě nesou společnou informaci, o složitější typ vztahu, kdy zjištěný souběh/protiběh variabilit způsobuje jiná proměnná působící na obě sledované, o nepřímý vztah zprostředkovaný další proměnnou (tzv. mediátor) nebo dokonce o náhodný souběh variabilit.

K analýze lze přistupovat dvěma základními způsoby. Explorační přístup data zkoumá a vytváří hypotézy, které by mohly vysvětlovat empiricky nalezené statistické vztahy. Naproti tomu konfirmační přístup vychází z určité představy o fungování vztahů, kterou se na základě dat snaží potvrdit nebo vyvrátit.

Korelační analýza má využití jednak sama o sobě pro analýzu vztahů mezi proměnnými, ale zároveň představuje také první stupeň analýzy pro další metody, které na ni navazují. Mezi ně patří například regresní analýza, faktorová analýza nebo strukturní modelování.

Přijďte si to vyzkoušet, naučíme Vás to

Pokud Vás korelační analýza zaujala, chcete porozumět jejím základům i hlouběji proniknout do její podstaty, rádi bychom Vás pozvali na kurz Korelační analýza. Představíme Vám korelační míry pro číselná data, jejich vlastnosti a aplikační využití v různých praktických situacích se zaměřením na interpretaci výsledků. Výuka bude probíhat za pomoci softwaru IBM SPSS Statistics.