Diskriminační analýza a logistická regrese II.

Klasifikace v lineární diskriminační analýze
V minulé části jsme se seznámili se vzorcem pro výpočet aposteriorní pravděpodobnosti (1) založeném na Mahalanobisovově vzdálenosti (2) a zmínili jsme, že vzorec se výrazně zjednoduší v případě lineární diskriminační analýze (dále DA). Vzorec se týká kanonických diskriminačních funkcí, které jsou popsány v minulém článku.
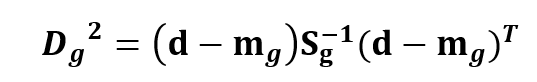
V lineární DA je vnitroskupinová kovarianční matice Sg stejná pro všechny skupiny a získá se průměrem z jednotlivých skupin. Společná matice je pro diskriminační proměnné rovna jednotkové, to je také jedním z důvodů, proč se vůbec diskriminační proměnné uvažují. Determinant jednotkové matice je jedna a inverzní matice je také jednotková, ve vzorcích matice zmizí a z Mahalanobisovovy vzdálenosti se stane Euklidovská.
Další zjednodušení vzorce (1) se získá, pokud jednu skupinu budeme považovat za referenční a její exponenciálu vytkneme v čitateli i jmenovateli. V exponentech je rozdíl vzdáleností dané a referenční skupiny, po roznásobení vzorce (2) a vyjádření rozdílu se druhé mocniny diskriminačních funkcí vyruší a zůstane jen lineární část. To je důvod, proč mluvíme o lineární DA. Pro přehlednost se apriorní pravděpodobnosti přesunou do exponentu a vzorec (1) přejde do následujícího tvaru.
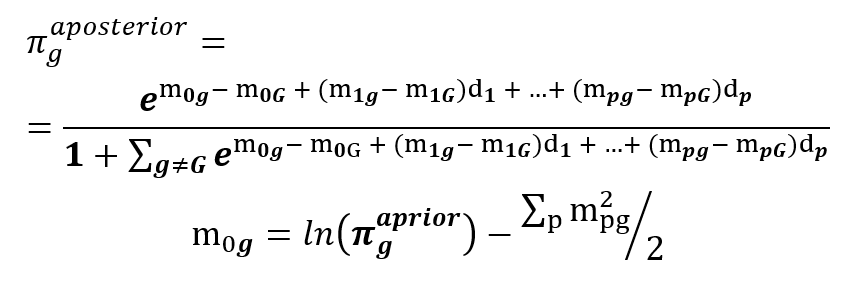
Aposteriorní pravděpodobnosti jsou určeny jen centroidy diskriminačních funkcí a apriorní pravděpodobností, ta ovlivňuje jen absolutní člen. Vzorec platí i pro referenční skupinu, v čitateli pak bude hodnota 1, protože se v exponentu vše odečte.
Nyní si můžeme objasnit zdánlivou dvojznačnost metody zmíněnou v prvním díle. Ve vzorci (3) se lze totiž vrátit k původním proměnným, stačí použít opačnou (inverzní) transformaci. Po úpravách se vrátíme k původním centroidům mg a k původní vnitroskupinové kovarianční matici S. Ta je stále společná pro všechny skupiny, ale už není jednotková, výpočet koeficientů bude proto složitější.
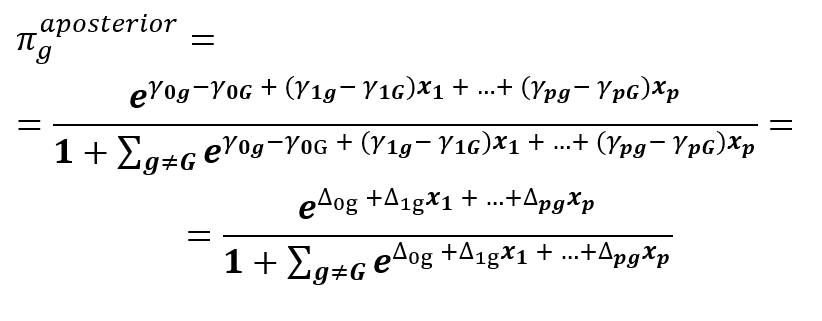
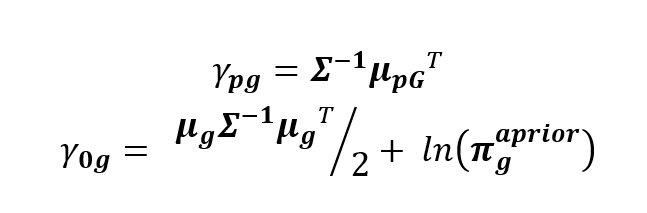
Formálně je vzorec (3) shodný se vzorcem (4), ale liší se výpočtem koeficientů a tím, že ve druhém jsou původní proměnné. V učebnicích se vzorec (4) odvozuje rovnou bez přechodu k diskriminačním funkcím, takže na první pohled není patrná jeho souvislost se vzorcem (3), ačkoliv dávají zcela stejné výsledky. Vzorec (4) se dá ještě po mírné úpravě napsat jinak, roznásobíme závorky a dáme k sobě členy pro počítanou a referenční skupinu. Jejich součet tvoří tzv. klasifikační funkci, někdy také nazývanou Fisherova diskriminační funkce, což je třeba odlišovat od dříve zmiňované kanonické diskriminační funkce.
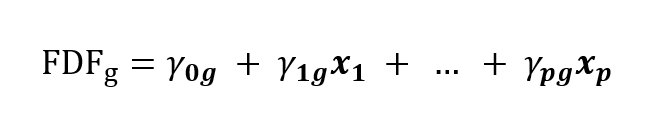
Klasifikační funkce bývá někdy samostatnou součástí výstupu diskriminační analýzy nebo je popsána v literatuře jako hlavní nástroj pro klasifikaci, ale stále jde jen o ekvivalentní výpočet ke kanonickým diskriminačním funkcím. Může se tedy nabízet otázka, proč vůbec používat kanonické diskriminační funkce, když lze klasifikaci provést pomocí klasifikační funkce a tu získat rovnou z původních proměnných pomocí vzorce (5). Jedním důvodem je jednodušší intepretace, se kterou se seznámíme v další části, ale také možnost některé diskriminační proměnné vypustit. K tomu jsou odvozené testy, které určí, zda je daná diskriminační funkce statisticky významná. Diskriminační funkce jsou navíc odvozeny tak, že jejich síla postupně klesá, někdy je tedy vhodné použít pouze několik prvních. Takové zjednodušení není při použití klasifikačních funkcí možné. Při použití menšího počtu diskriminačních funkcí vyjdou aposteriorní pravděpodobnosti odlišně a už se nerovnají těm vypočteným podle klasifikačních funkcí. Rozdíly ale nejsou v praxi příliš velké. V další části se pokusím dát klasifikaci věcnou interpretaci.
Interpretace
Nyní se můžeme pokusit dát význam koeficientům ve vzorci pro aposteriorní pravděpodobnost, a to v obou variantách výpočtu (3) a (4).
V LDA je interpretace koeficientů obtížnější, neexistuje jasná statistická intepretace, nejjednodušší je dát koeficientům geometrickou intepretaci. Ta je dvojí, protože LDA provádí výpočet aposteriorní pravděpodobnosti dvěma způsoby, které vedou ke stejnému výsledku. V obou způsobech jsou klíčové centroidy srovnávaných skupin.
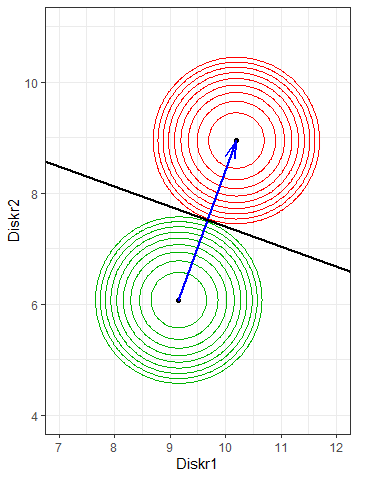
V prvním způsobu jsou vysvětlující proměnné lineárně transformovány na diskriminační skóre, které lépe rozlišuje jednotlivé skupiny. Z diskriminačních skóre skupin se spočítají centroidy a přímky, podél kterých jsou aposteriorní pravděpodobnosti rovné určité hodnotě, jsou kolmé na spojnici centroidů, jejich pozice závisí také na apriorních pravděpodobnostech. Při stejných apriorních pravděpodobnostech a hraniční pravděpodobnosti 0.5 je případ přiřazen ke skupině s bližším centroidem. Na Obr. 1. jsou v prostoru diskriminačních funkcí zobrazeny dva centroidy s kružnicemi vyznačujícími vzdálenost. Hraniční přímka je kolmá ke spojnici centroidů.
To je základní myšlenka LDA, spočítat lépe rozlišující diskriminační funkce a v nich případ přiřadit k nejbližšímu středu skupiny se započítáním apriorních pravděpodobností.
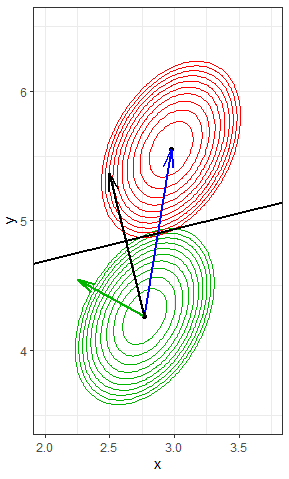
Ve druhém způsobu se pracuje s původními proměnnými. Spojnici centroidů v prostoru diskriminačních funkcí lze zpětně transformovat do prostorů původních proměnných. Transformovaná spojnice už nespojuje centroidy původních proměnných, ale její směr je ovlivněn i vnitroskupinovou kovariancí proměnných. Je natočena do směru, ve kterém má vzdálenost k centroidu nejmenší rozptyl (viz Obr. 2), konkrétní míra otočení závisí na samotné vnitrokovarianční matici a poloze centroidů. Přímky konstantních aposteriorních pravděpodobností jsou kolmé na otočenou spojnici, jejich poloha opět závisí na apriorních pravděpodobnostech. Pokud jsou apriorní pravděpodobnosti stejné, je případ přiřazen k bližšímu centroidu, ale podle Mahalanobisovovy vzdálenosti.
Nyní lze konečně najít význam koeficientů klasifikačních funkcí, přesněji řečeno rozdílu hodnot funkcí pro dvě skupiny. Rozdíly koeficientů klasifikačních funkcí pro srovnávané skupiny u proměnné p jsou koeficienty přímky s konstantními aposteriorními pravděpodobnostmi u této proměnné.
Rádi byste se o statistice a analýze dat dozvěděli více? Chcete se stát mistrem ve svém oboru nebo si jen potřebujete doplnit znalosti? V ACREA nabízíme širokou nabídku kurzů pro váš profesní růst. Máte-li jiný dotaz. Nebojte se využít naši nezávaznou konzultaci, při které vám rádi zodpovíme všechny vaše dotazy a najdeme vhodné řešení.