Diskriminační analýza a logistická regrese I.

Jednou z velmi častých úloh statistiky i datascience je klasifikace. Úloha spočívá v odhadu skupiny (třídy), ke které případ náleží na základně jeho vlastností zachycených sadou číselných i kategorizovaných proměnných. Ty budeme nazývat vysvětlující. V úloze se například určuje diagnóza pacienta podle výsledků vyšetření nebo budoucí platební morálka klienta banky podle jeho sociodemografických a finančních charakteristik. Úlohu lze řešit mnoha metodami, ale ke klasickým statistickým metodám patří logistická regrese a diskriminační analýza (DA). V této sérii se zaměříme na způsob, jakým dochází ke klasifikaci v diskriminační analýze, jak interpretovat působení vysvětlujících proměnných a srovnáme způsob klasifikace s logistickou regresí. Pro obecnost budeme předpokládat existenci více než dvou skupin, což je typická úloha diskriminační analýzy, logistická regrese pro více skupin se nazývá multinomická (MLR).

Základní pojmy a varianty diskriminační analýzy

Základní myšlenka diskriminační analýzy je založena na vzdálenosti. Při klasifikaci případu se porovnává vzdálenost k centrům jednotlivých skupin a případ se klasifikuje do skupiny, ke které má v jistém smyslu nejblíže. Celý postup je ale komplikovanější než pouhý výpočet vzdáleností.

Pro klasifikaci jsou důležité tři pojmy prostupující celou DA.

• Centroid – tvoří jej průměrné hodnoty vysvětlujících proměnných v dané skupině, existuje vždy jeden centroid pro každou skupinu a má tolik složek, kolik je proměnných.
• Vnitroskupinová kovarianční matice – matice obsahuje na diagonále rozptyly a mimo ni kovariance jednotlivých proměnných, zásadní je, že se počítá pro každou skupinu zvlášť. V jednodušší variantě DA se pak matice zprůměrují za všechny skupiny, ve složitější se pracuje s maticemi za jednotlivé skupiny.
• Apriorní pravděpodobnosti – pravděpodobnost určuje příslušnost případu ke skupině bez ohledu na jeho vysvětlující proměnné. Obvykle vychází z populačních četností nebo je odhadnuta z četností v datovém souboru. Každá skupina má jednu hodnotu a součet přes skupiny je 1.

Pro uživatele DA může být matoucí, že v literatuře je často popis dvou metod a v softwarech jsou někdy implementovány dva způsoby klasifikace, aniž by byl mezi nimi na první pohled jasný vztah. Ve skutečnosti jde jen o jednu metodu, která má složitou a zjednodušenou verzi. Zjednodušená verze klasifikace v DA se dá upravit tak, že na první pohled vypadá jako samostatná metoda. Výsledky obou způsobů úpravy výpočtu jsou samozřejmě stejné. Složitá varianta žádné alternativní vyjádření nemá.

Rozdíl mezi složitou a jednoduchou verzí spočívá v práci s vnitroskupinovou kovarianční maticí. Ve složitější verzi se uvažuje zvláštní matice pro každou skupinu, mluvíme pak o kvadratické DA. Ve zjednodušené verzi se pracuje s průměrem z vnitroskupinových kovariančních matic, takže je jen jedna, což vše zásadně zjednoduší. V tomto případě se jedná o lineární DA (LDA). V následujícím textu se zatím přidržíme obecného postupu a na vhodném místě popíšeme i modifikaci postupu v LDA.

Klasifikace v Diskriminační analýze

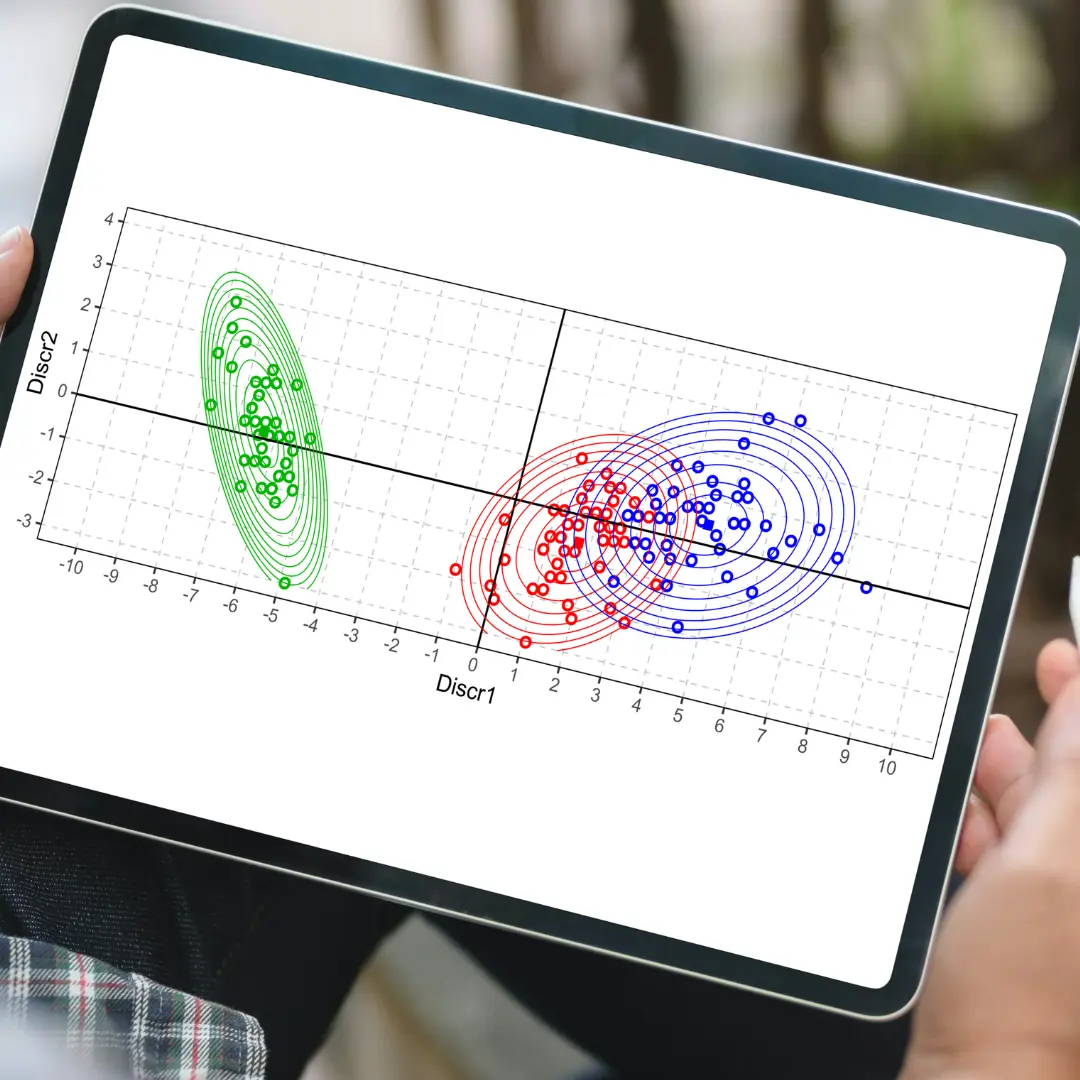
Základní myšlenka DA, porovnávat vzdálenost k centroidům skupin, je modifikována použitím kanonických diskriminačních funkcí. Jedná se o nové proměnné, které se počítají z původních vysvětlujících proměnných. Idea odvození nových proměnných je, aby se hodnoty těchto proměnných co nejvíce lišily mezi skupinami. Transformace původních na nové proměnné se omezuje na lineární funkce, původní proměnné se vynásobí vhodnými koeficienty a posčítají dohromady. Odhad koeficientů se získá z celkové a vnitroskupinové kovarianční matice hledáním tzv. vlastních čísel a vektorů. Detaily výpočtu koeficientů nejsou pro pochopení klasifikace důležité, podstatné je, že vzniknou nové proměnné, s jejichž využitím je klasifikace jednodušší. Počet proměnných může být nejvýše roven počtu původních proměnných nebo počtu skupin mínus 1, platí to menší. Pro každý případ se spočítají hodnoty kanonických diskriminačních funkcí a z nich se spočítají kanonické centroidy a kanonické vnitroskupinové kovarianční matice.

Klasifikace je realizována výpočtem aposteriorních pravděpodobností příslušnosti ke skupině. Aposteriorní pravděpodobnosti vycházejí z apriorních, ale jsou upraveny podle vzdáleností k centroidům skupin. Při výpočtu se vychází z představy, že původní proměnné mají vícerozměrné normální rozdělení. Pak lze spočítat pravděpodobnost, že případ patří k určité skupině, pokud od ní má danou vzdálenost. Z této pravděpodobnosti a apriorní pravděpodobnosti se podle Bayesova vzorce spočítá pravděpodobnost aposteriorní.

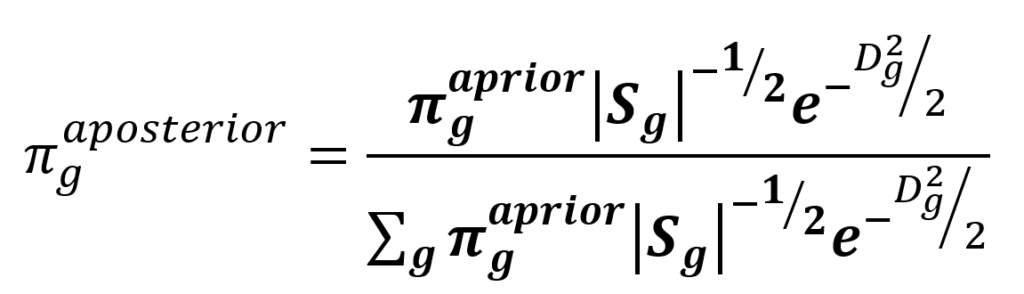
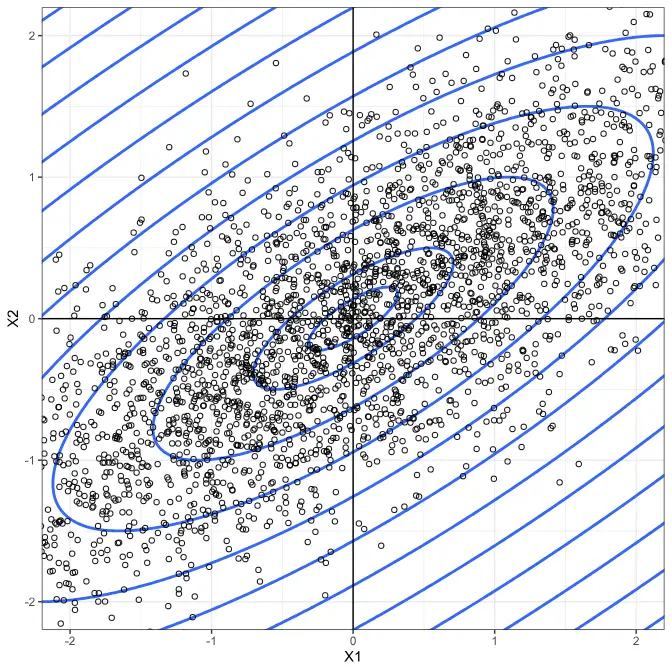
Ve vzorci 1 vystupují determinanty vnitroskupinových kovariančních matic S_g a vzdálenosti D_g od centroidů skupiny g, vše se týká diskriminačních funkcí. Vzdálenost ve vzorci ale není ta běžná tedy Euklidova, ale Mahalanobisovova. Ta zohledňuje směry, do kterých jsou případy ve skupinách rozptýlené. Obr. 1 zachycuje elipsy konstantní Mahalanobisovovy vzdálenosti od centroidu. Ve směru s větším rozptylem dosahuje daná hodnota Mahalanobisovovy vzdálenosti dále od středu, měřeno běžnou vzdáleností. Vzorec 2 ukazuje její výpočet, figuruje v něm vnitroskupinová kovarianční matice a centroidy.

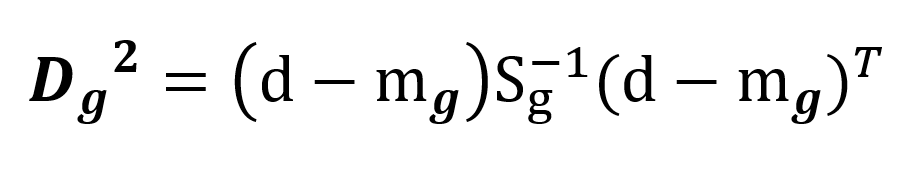
V lineární DA se vzorce 1 a 2 výrazně zjednoduší. Diskriminační funkce mají totiž tu vlastnost, že průměrná vnitroskupinová kovarianční matice S_g je jednotková, takže z obou vzorců kovarianční matice zmizí a Mahalanobisovova vzdálenost se změní na obyčejnou Euklidovu.

V další části si ukážeme, jak v lineární DA vzorec 1 upravit, přetransformovat do zdánlivě nesouvisejících funkcí a provést podle něj klasifikaci do skupin. Transformace pak také umožní intepretaci koeficientů v DA.

Rádi byste se o statistice a analýze dat dozvěděli více? Chcete se stát mistrem ve svém oboru nebo si jen potřebujete doplnit znalosti? V ACREA nabízíme širokou nabídku kurzů pro váš profesní růst. Máte-li jiný dotaz. Nebojte se využít naši nezávaznou konzultaci, při které vám rádi zodpovíme všechny vaše dotazy a najdeme vhodné řešení.