Jedním z předpokladů T-testů (parametrických testů) je, že proměnná, kterou analyzujeme, pochází z populace s normálním rozdělením. Než tento test použijeme, měli bychom ověřit, zda je daný předpoklad splněn.

V tomto článku se budeme věnovat situaci, kdy zjistíme, že tomu tak není. V takovém případě je možné řešení použití tzv. distribution-free testu, tedy testu nezávislého na rozdělení – jinými slovy, neparametrického testu.

Kdy sáhneme po neparametrických testech?

• V situaci, kdy nejsou splněny předpoklady parametrických testů.
• Pokud chceme otestovat jinou hypotézu než hypotézu o parametru rozdělení.
• Když testovaná proměnná není číselná, ale například ordinální.

Jaké jsou jejich výhody a nevýhody?

Výhody:

• Nezávislost na rozdělení dat
  Na rozdíl od parametrických testů, které předpokládají normální rozdělení dat, neparametrické testy tyto předpoklady nemají. Díky tomu je lze použít i u dat, která nejsou normálně rozložena nebo u kterých rozdělení neznáme.
• Větší odolnost vůči odlehlým hodnotám
  Neparametrické testy jsou robustnější při výskytu extrémních hodnot, protože často pracují s pořadím hodnot (ranky) místo jejich konkrétních číselných hodnot. To znamená, že výsledky testu nejsou tolik ovlivněny několika málo výrazně odlišnými pozorováními.
• Výpočetně jednodušší
  Neparametrické testy obvykle nevyžadují složité matematické operace ani odhady parametrů (např. průměr či směrodatná odchylka), takže jsou výpočetně méně náročné.

Nevýhody:

• Testují jinou hypotézu než parametrické testy
  I když jsou často prezentovány jako alternativy k parametrickým testům, neparametrické testy ve skutečnosti testují odlišné hypotézy. Například místo hypotézy o rovnosti průměrů testují hypotézy o rozdílu v mediánech nebo v rozložení pořadí hodnot. To je důležité mít na paměti při interpretaci výsledků. Jaké konkrétní hypotézy testují, si podrobněji vysvětlíme dále v článku.
• Nižší síla testu
  Absence předpokladů o rozdělení dat s sebou nese nevýhodu v podobě nižší statistické síly testu. To znamená, že je vyšší pravděpodobnost, že test nezamítne nulovou hypotézu, i když ve skutečnosti není pravdivá. Jinými slovy, je větší riziko chyby II. druhu.

Které neparametrické testy se běžně používají?

Neparametrické alternativy k dvouvýběrovému t-testu
Pokud nejsou splněny předpoklady parametrického dvouvýběrového t-testu, lze použít neparametrické testy. Nejčastěji se využívá Mann-Whitneyho U test, jehož nulová hypotéza říká, že obě testované skupiny mají stejné rozdělení. Alternativou je také mediánový test, který testuje, zda se mediány ve skupinách statisticky liší. Výběr testu závisí na tom, jakou hypotézu chceme testovat – shodu rozdělení nebo shodu mediánů.

Neparametrické alternativy k analýze rozptylu (ANOVA)
Pokud nejsou splněny předpoklady pro použití jednofaktorové ANOVY (např. normalita dat či shoda rozptylů), lze využít neparametrické testy. Nejčastější volbou je Kruskal-Wallisův test, který – podobně jako Mann-Whitneyho test – porovnává rozložení hodnot mezi více než dvěma skupinami. Nulová hypotéza předpokládá, že rozdělení ve všech skupinách je stejné. Alternativně lze použít i mediánový test, který umožňuje testovat shodu mediánů napříč více skupinami. Výběr závisí opět na povaze dat a konkrétní testované hypotéze.

Neparametrické alternativy k párovému t-testu
Pokud nejsou splněny předpoklady pro použití párového t-testu, lze využít Wilcoxonův párový test. Tento test porovnává rozdíly mezi dvěma spárovanými výběry a zjišťuje, zda mediány těchto rozdílů jsou nulové. Nulová hypotéza předpokládá, že obě pozorované veličiny pochází z rozdělení se stejným mediánem. Wilcoxonův test je vhodný pro ordinální data nebo data s odlehlými hodnotami, kde by použití parametrických metod mohlo vést ke zkresleným výsledkům.

Ukázka výpočtu Kruskal-Wallisova testu v IBM SPSS Statistics

K dispozici máme data přibližně od 2000 respondentů, kteří hodnotili, jak vnímají současný stav školství. Hodnocení probíhalo na ordinální škále od 0 do 10, kde vyšší hodnota značí pozitivnější vnímání. Cílem analýzy je zjistit, zda se vnímání školství liší v závislosti na věku respondentů.
Věk respondentů byl rozdělen do tří věkových kategorií:

• 15–35 let
• 36–55 let
• 56 let a více

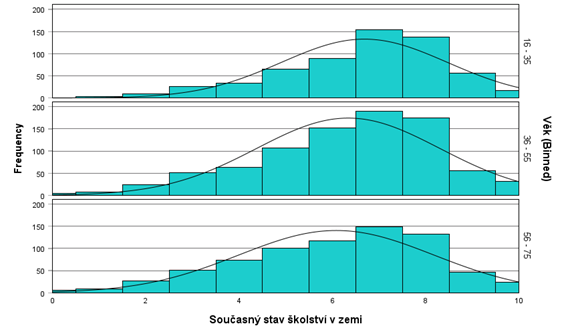
Porušení předpokladu normality dokládá také histogram níže. Z tohoto důvodu bude pro analýzu rozdílů ve vnímání školství mezi věkovými skupinami využit Kruskal-Wallisův test, který nevyžaduje normalitu dat a je vhodný pro porovnání více než dvou nezávislých skupin.

Volání procedury v IBM SPSS Statistics

Analyze → Nonparametric Tests → Independent Samples

Nastavení dialogu

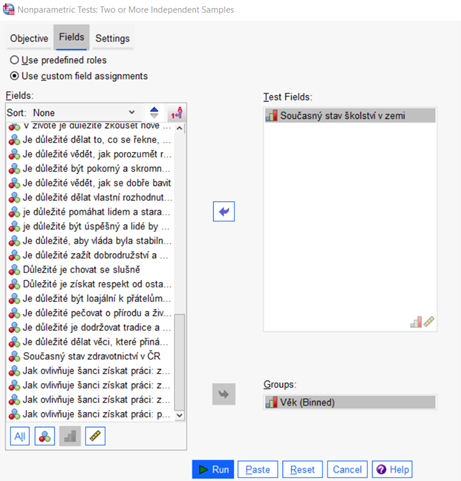
Nejprve na záložce Fields vyplníme testované proměnné. Do okna Test Fields vložíme ordinální proměnnou Současný stav školství v zemi a do pole Groups proměnnou Věk, která určuje rozdělení pozorování do skupin.

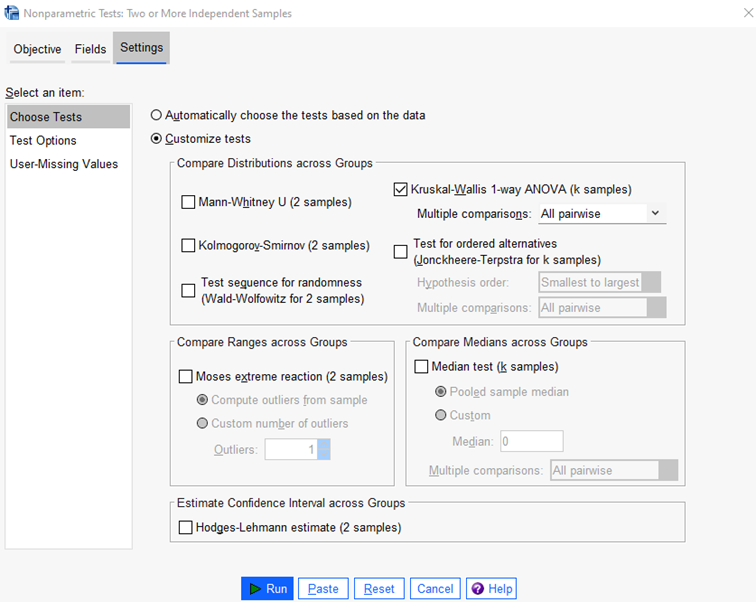
Dále na záložce Settings klikneme na možnost Customize tests, což nám umožní vybrat konkrétní statistický test. Pro danou úlohu máme na výběr dvě možnosti: Kruskal-Wallisův jednofaktorový ANOVA test nebo mediánový test. V tomto článku se zaměříme pouze na Kruskal-Wallisův test. Poté klikneme na tlačítko Run a ve výstupním okně se nám vygeneruje několik výstupů.

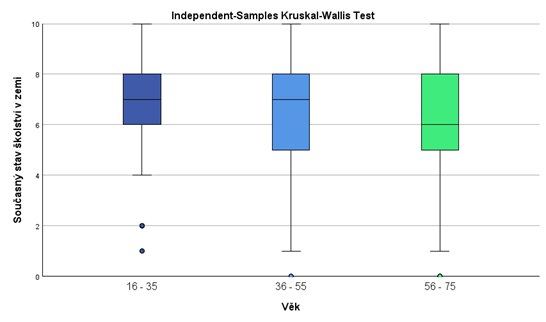
Prvním výstupem je boxplot pro jednotlivé skupiny. Na první pohled si můžeme všimnout, že medián u nejstarší skupiny respondentů je nejnižší, což naznačuje, že současný stav školství vnímají nejhůře ze všech sledovaných skupin.

Je však důležité si uvědomit, že námi zvolený test netestuje shodu mediánů, ale ve své nulové hypotéze testuje shodu rozdělení mezi skupinami.

O výsledku testu nás informuje následující tabulka. Kromě zopakování testované hypotézy a hladiny významnosti v ní najdeme i samotný závěr: na hladině významnosti 5 % zamítáme nulovou hypotézu o shodě rozdělení mezi skupinami.

V další části výstupu se můžeme podívat na výsledky tzv. párového srovnání, při kterém byly všechny skupiny porovnány mezi sebou.

Ze tří testovaných dvojic se mezi sebou statisticky významně liší dvě (viz sloupec Adj. Sig). Konkrétně jde o nejstarší skupinu ve srovnání s nejmladší a nejstarší skupinu ve srovnání s kategorií 36–55 let. Mezi kategoriemi 16–35 a 36–55 let nebyl zjištěn statisticky významný rozdíl.

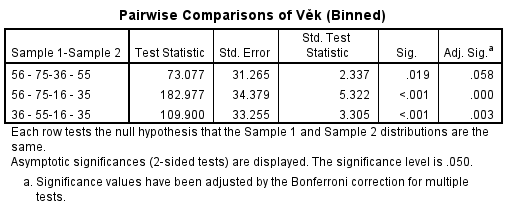
Výsledky uvedené v tabulce Pairwise Comparisons jsou dále vizualizovány pomocí spojnicového grafu, kde jsou statisticky významné rozdíly zvýrazněny modrou barvou.

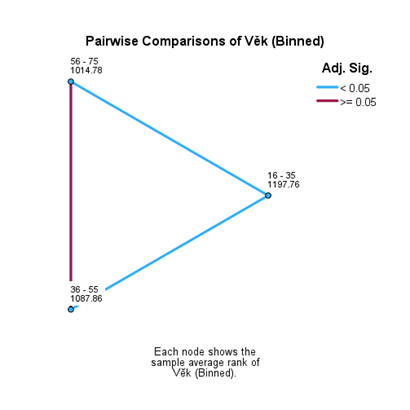
Neparametrické testy představují důležitý nástroj v situacích, kdy data nesplňují předpoklady klasických (parametrických) metod – například normalitu rozdělení nebo homogenitu rozptylů. Díky své flexibilitě umožňují analyzovat širokou škálu dat, a to i v případech, kdy je datový soubor menší nebo obsahuje odlehlé hodnoty. Testy jako Kruskal-Wallisův test nebo mediánový test nám poskytují spolehlivé výsledky i tam, kde by parametrické metody mohly selhat.

Zaujala vás problematika a chcete se dozvědět více?

Objevte principy neparametrických testů – ideální řešení, když nejsou splněny předpoklady pro parametrické testy. Naučte se je používat v praxi.

Přihlaste se ještě dnes