Bayesovský odhad přesnosti antigenních testů

Otestoval jsem se antigenním testem s pozitivním výsledkem. Jaká je pravděpodobnost, že jsem skutečně nakažen? Mám se orientovat podle senzitivity nebo specificity testu?

Nejprve si krátce připomeňme, co senzitivita a specificita testu vyjadřují, podrobnější popis můžete najít v příspěvku Lubomíry Červové s názvem „Víte, jak se hodnotí validita diagnostických testů (nejen) na COVID 19?“. Výsledek testu je pozorovaná dvoustavová veličina, může být pozitivní, nebo negativní. Skutečná nákaza covid-19 je také dvoustavová, avšak nepozorovaná, veličina. Jedinec může být zdravý, nebo nakažený. V optimálním případě by měl výsledek testu být ve shodě s nákazou. Testy ale nejsou dokonalé a souvislost mezi výsledkem testu a nákazou měříme na reprezentativním výběru z populace, výsledky ukládáme do následující čtyřpolní tabulky. V řádcích jsou kategorie nákazy, ve sloupcích výsledky testu. Do buněk tabelujeme počty jedinců. Počty můžeme transformovat na procenta v rámci řádku, procenta v rámci sloupce nebo procenta v celé tabulce.

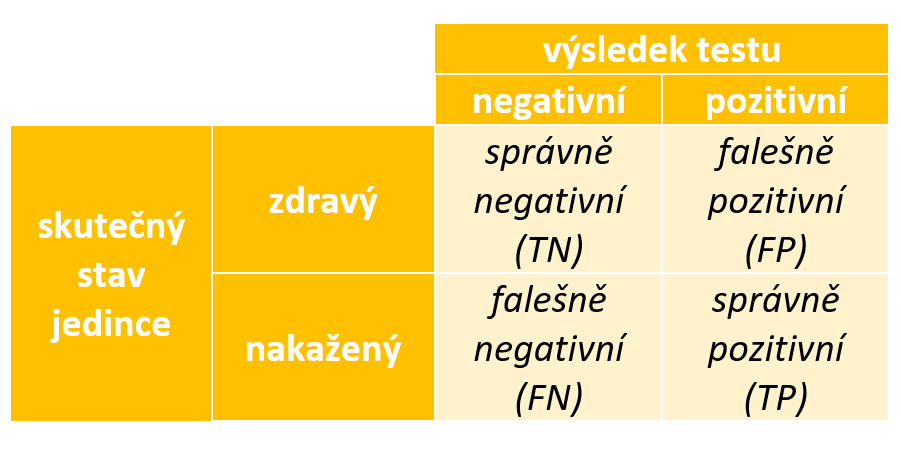
Senzitivita testu je řádkové procento nakažených jedinců s pozitivním testem. Vyjadřuje, jaký podíl nakažených odhalí test. Doplněk senzitivity pak určí, jaký podíl nakažených jedinců projde testováním bez povšimnutí.

Specificita testu je řádkové procento zdravých jedinců s negativním testem. Ukazuje, jaký podíl zdravých jedinců projde testem. Doplněk specificita pak vyjadřuje podíl falešné pozitivity, tj. kolik procent zdravých musí nastoupit do karantény.

Doplňky senzitivity a specificity ukazují na podíly nežádoucích chyb testu v populaci. Pro otestovaného jedince však tato čísla nejsou příliš informativní, není z nich na první pohled vidět, jaká je pravděpodobnost nákazy, pokud jsem pozitivně otestován, resp. jaká je pravděpodobnost, že jsem zdráv, pokud test vyšel negativně. K tomu bychom potřebovali spočítat sloupcová procenta v naší čtyřpolní tabulce.

Výrobci testů však uvádějí jen senzitivitu a specificitu. Senzitivita a specificita jsou neměnné parametry testu, požadovaná sloupcová procenta závisí i na podílu nakažených v populaci, a proto je ani nemá smysl u testů uvádět. Naštěstí můžeme využít Bayesův vzorec pro podmíněnou pravděpodobnost, jenž nám umožní spočíst požadovanou přesnost testu za dané epidemiologické situace. Přesností testu budeme rozumět pravděpodobnost nákazy u pozitivně otestovaného jedince.

Bayesův vzorec je velmi jednoduchý, jedná se o formální úpravu vzorce pro podmíněnou pravděpodobnost. V našem případě umožní vypočítat pravděpodobnost nákazy pro pozitivně testované jedince, pokud známe pravděpodobnost pozitivního výsledku testu u nakažených jedinců. A pravděpodobnost pozitivního výsledku testu u nakažených známe, je jí udávaná senzitivita.

Označme p(N|T) hledanou přesnost testu, tj. pravděpodobnost nákazy u pozitivně otestovaných jedinců. Senzitivitu zapíšeme jako p(T|N), tj. pravděpodobnost pozitivního výsledku testu u nakažených. Specificitu označíme pomocí p(T´|N´), čárky nad symboly pro test a nákazu označují negaci, v našem případě negativní výsledek testu a nenakaženého jedince.

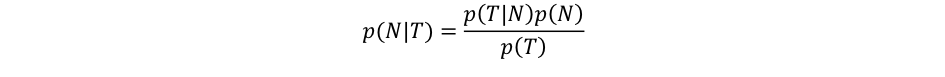
V Bayesově vzorci se na pravé straně kromě senzitivity p(T|N) vyskytují i nepodmíněné pravděpodobnosti p(N) a p(T). p(N) je podíl nemocných v populaci označovaný epidemiology jako prevalence. Prevalence populace ČR se běžně neuvádí, ale na denní bázi je veřejně prezentována incidence. Ta udává počet nově nemocných na 100 000 obyvatel během uplynulého týdne či čtrnácti dnů. Pokud připustíme, že virové onemocnění způsobené covidem-19 trvá dva týdny, čtrnáctidenní incidence může být po krátké diskusi dosazena za p(N).

Současná hodnota čtrnáctidenní incidence v celé ČR je přibližně 20 případů na 100 000 obyvatel (0,02 %). V době vrcholné pandemie byla incidence na úrovni okolo 1500 případů na 100 000 obyvatel (1,5 %), tj. 75krát vyšší než dnes.

p(T) v Bayesově vzorci udává podíl pozitivně testovaných. Toto číslo se též zveřejňuje na denní bázi, dokonce bývá udáváno pro různé důvody pro testování (indikace) nebo zvlášť pro antigenní a PCR testy. Zatímco v pandemických špičkách podíl kladně testovaných u medicínské indikace atakoval 50% hladinu, dnes se pohybuje na hodnotách okolo 1 %.

Reportovaný podíl pozitivně otestovaných p(T)však není vhodná reprezentativní hodnota pro dosazení do Bayesova vzorce. Testované jedince nemůžeme považovat za náhodný výběr z populace. Testovat se chodíme z různých důvodů, nikoli náhodně. Přímým dosazením do vzorce se dopustíme značné chyby. Abychom získali přesnost testu pro náhodně otestovaného jedince, vyjádříme si podíl pozitivně otestovaných p(T) pomocí vzorce pro úplnou pravděpodobnost.

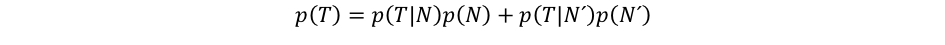
Jedná se o elementární rozpis nepodmíněné pravděpodobnosti pomocí součtu podmíněných pravděpodobností. V našem případě, kdy jedinec může být nakažený, nebo zdravý, potřebujeme dva sčítance. Ve vyjádření p(T) se objevuje prevalence p(N) a také její doplněk p(N´), tyto hodnoty již máme k dispozici. Známe také senzitivitu testu p(T|N), pravděpodobnost p(T|N´) je pak doplňkem specificity a tu známe také.

Po dosazení do vzorce pro úplnou pravděpodobnost a do Bayesova vzorce získáme na první pohled překvapivé hodnoty přesnosti testu. Přesnost testu, tj. pravděpodobnost nákazy u jedince s pozitivním testem, závisí nejen na senzitivitě a specificitě testu, ale i na aktuální epidemiologické situaci, konkrétně na podílu nakažených v populaci p(N). Následující graf ukazuje, jak se mění přesnost běžného antigenního testu se senzitivitou 90 % a specificitou 95 % pro různé hodnoty prevalence.

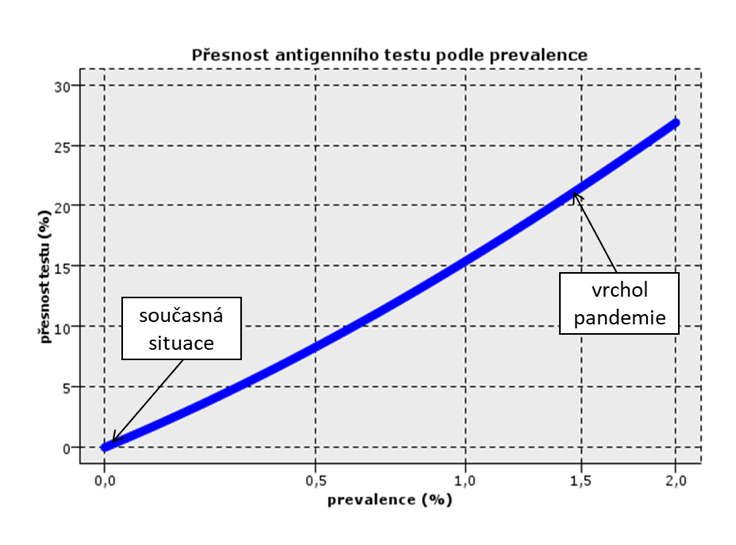
V dobách vrcholného rozšíření koronaviru, kdy se prevalence p(N) pohybovala okolo 1,5 %, byla přesnost antigenního testu pouze 21,5 %. Dnes, kdy prevalence klesla hluboko pod jedno promile, je přesnost antigenního testu ještě výrazně menší, dostala se pod 0,4 %. Po pozitivním otestování antigenním testem mohu s 99,6 % jistotou tvrdit, že jsem zdráv.

Má smysl se testovat, když pravděpodobnost, že jedinec s pozitivním testem je skutečně nemocný, je tak nízká? Spočtené hodnoty si zaslouží několik komentářů, abychom byli schopni otázku zodpovědět.

1. Přesnosti byly spočteny za předpokladu, že se nechám otestovat zcela náhodně, tj. bez ohledu na to, zda mám, či nemám příznaky, na test mě posílá lékař či hygienik, nebo že se musím testovat na základě nějakého předpisu.
2. Užitečnost antigenních testů bychom měli posuzovat poměrem. Pozitivně otestovaní jedinci mají sice nízkou pravděpodobnost nákazy, avšak neotestovaní jedinci mají pravděpodobnost nákazy ještě výrazně nižší. Například v současnosti je pravděpodobnost nákazy u pozitivně otestovaných 20krát vyšší než u jedinců neotestovaných (0,4 % / 0,02 %). Test tak umožní separovat osoby s řádově vyšším rizikem.
3. Analyzovanou přesnost testu p(N|T) ovlivňuje jeho senzitivita a specificita a také prevalence. Konkrétní vliv těchto faktorů popisuje uvedený Bayesův vzorec a vzorec pro úplnou pravděpodobnost. Pokud bychom chtěli přesnost testu výrazně zvýšit a víme, že prevalence p(N) je malé číslo, měli bychom se zaměřit především na zvyšování specificity. Zvýšení senzitivity bude mít na přesnost testu jen nepatrný vliv. Nízká pravděpodobnost, že pozitivně otestovaný jedinec je skutečně nakažený, je především důsledkem toho, že v populaci výrazně převládají zdraví jedinci, a díky nedokonalé specificitě někteří z nich vyjdou v testu jako pozitivní. Pokud si chcete být jistější, že při pozitivním výsledku testu máte covid-19, vybírejte si test s co nejvyšší specificitou.

Podobně, jako jsme si rozebrali přesnost testu, která vyjadřuje pravděpodobnost nákazy u osob s pozitivním výsledkem, mohli bychom se zabývat otázkou: Jaká je pravděpodobnost, že jsem zdravý, pokud mi vyšel antigenní test negativně? Postupovali bychom analogicky. Pomocí Bayesova vzorce a vzorce pro úplnou pravděpodobnost lze tuto podmíněnou pravděpodobnost p(N´|T´)vyjádřit pomocí senzitivity a specificity testu a prevalence. I zde závěr vychází na první pohled překvapivě, a to opět díky nízké prevalenci p(N). I pro nízké hodnoty senzitivity a specificity bude pravděpodobnost p(N´|T´)velmi blízko 100% hladině. Například pro antigenní test z našeho příkladu se senzitivitou 90 % a specificitou 95 % a při prevalenci 0,02 % odpovídající současnému stavu pandemie v ČR si můžeme po negativním otestování být na 99,98 % jisti, že jsme zdrávi.