Jak velký má být můj výzkumný soubor?

Analytik resp. statistik dostává zřejmě nejčastěji otázky typu: Jak mohu zpracovat má data? Co mohu zjistit z mých dat? Případně dostává úkol: Zjistěte souvislost všeho se vším. Je nasnadě, že jde o nadlidský úkol, analytik/statistik nadto často věcně zkoumané oblasti nerozumí a v tom, co se bude zkoumat, by měl mít primárně jasno výzkumník, který výzkum vymyslel a realizuje. Velice často kladenou otázkou (byť méně často, než by bylo žádoucí) je: Jak velký soubor dat mám získat? Tato otázka není často pokládána, protože proto, že výzkumníci užívají zvyková pravidla typu: 100 jednotek je správně, 200 jednotek je správně, 300 jednotek apod. Tato pravidla jsou značně sporná a v mnoha situacích spíše neplatí, než platí. Proto lze doporučit, aby tato zvyková pravidla nebyla uplatňována a bylo užíváno sofistikovanějších přístupů. Ještě dříve, než tyto přístupy stručně popíšeme, rozeberme některá další sporná doporučení. Jako poměrně rozšířená doporučení (zejména v knihách) lze nalézt tabulky, které odvozují velikost výběru od velikosti populace. Tyto tabulky jsou velice populární a jsou přetiskovány bez jakékoli kritické reflexe do dalších knih. Jako ukázku zcela bizardního doporučení lze uvést, že v těchto tabulkách se radí, že pokud máme populaci o velikosti 30, má být náš výběr veliký 28 jednotek; pro populace o 60 jednotkách potřebuji výběr o velikosti 52 jednotek.
Zkusme nyní trošku precizněji popsat soudobé přístupy ke stanovení velikosti výzkumného souboru a stručně je představit. Pokud chceme určit velikost výzkumného souboru, musíme mít poměrně jasno o konci našeho výzkumného snažení, tj. o prováděných analýzách. Logicky se nabízí otázka, jak mohu mít před započetím výzkumu jasno o tom, jaké analýzy budu provádět na jeho konci. Dodejme, že pokud chci provádět konfirmační kvantitativní studii, pak bych měl mít jasnou výzkumnou otázku a z ní plynoucí výzkumné hypotézy. Právě tyto hypotézy generují potřebu konkrétních analytických postupů. Tedy již na počátku (před započetím sběru dat) poměrně přesně vím, jaké analytické postupy budu používat a tato znalost mi může pomoci správněji stanovit velikost výzkumného souboru. Na tomto místě doplňme, že pokud budu provádět deskriptivní studii či studii exploračního typu, výše uvedené neplatí a pro stanovení velikosti výzkumného souboru nemusím a ani nemohu složitější postupy používat. Obdobně platí, že dále uvedené postupy jsou určeny pro náhodné výběry či randomizované experimenty, pro záměrné výběry či experimenty bez randomizace se tyto postupy použít nedají.
Doplňme ještě, že kromě představy o plánovaných analytických procedurách potřebuji znát i některé další skutečnosti. Klíčové je zejména to, zda budu analyticky pracovat s celým výzkumným souborem najednou, nebo zda jej budu chtít analyzovat po jednotlivých podskupinách (druhá strategie samozřejmě navyšuje požadavek na velikost výběrového souboru).
Nyní nahlédneme do logiky sofistikovanějších postupů. V zásadě existují dva rozšířenější přístupy pro stanovení velikosti výzkumného souboru:
a) Přístup založený na minimální požadované síle testu
b) Přístup založený na maximální požadované šířce intervalu spolehlivosti
a) Přístup založený na síle testu
První přístup je tradičnější a užívanější, mezi jeho čelního propagátora patří zejména Cohen (Cohen 1988). Logika tohoto přístupu je v zásadě snadná. Stanovíme si minimální velikost pro sílu statistického testu[1] (Cohen doporučoval 0,8), odhadneme, jaké výsledky získáme a z těchto veličin buď skrze speciální tabulky (grafy) nebo skrze software zjistíme minimální velikost výzkumného souboru. Pro ilustraci můžeme použít graf pro korelace, kde na ose x je vynesena velikost výběrového souboru, na ose y odpovídající síla testu a jednotlivé křivky jsou pro úroveň korelace 0,2 a 0,4.
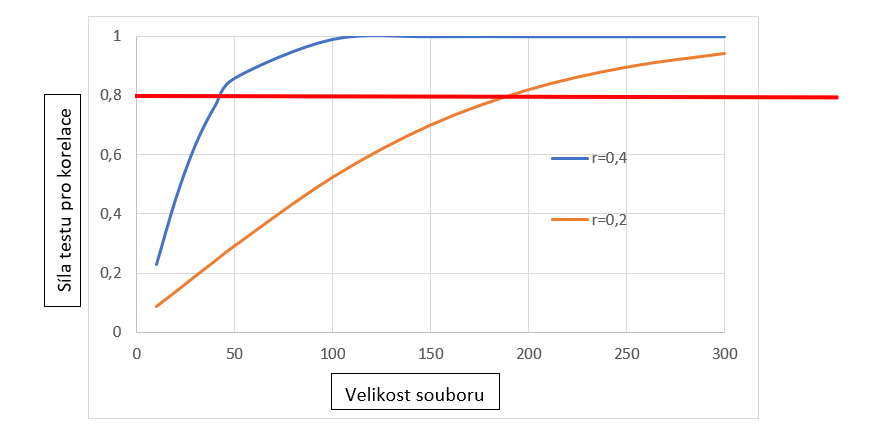
Z obrázku je patrné (viz červená čára na úrovni síly testu 0,8), že pokud očekávám korelaci o hodnotě cca 0,2, pak pro dosažení síly testu o hodnotě 0,8 a vyšší potřebuji téměř 200 výzkumných jednotek. Pokud očekávám korelaci vyšší (v našem grafu o hodnotě 0,4) je potřeba výrazně méně výzkumných jednotek (cca 45).
b) Přístup založený na intervalech spolehlivosti
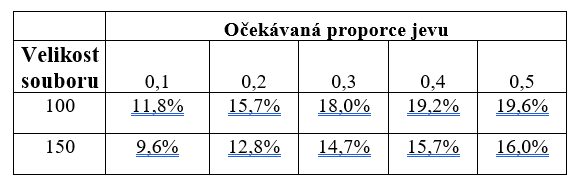
Druhý přístup je poněkud méně užívaný, ale pro běžné analytiky a výzkumníky zřejmě srozumitelnější než přístup založený na síle testu. Nadto v poslední době sílí požadavky na využívání intervalů spolehlivosti, lze tedy čekat, že tento přístup bude stále populárnější. Jako jeho hlavní propagátor může být označen Cumming (Cumming & Jageman, 2017). Tento přístup vychází z toho, že analytik dopředu opět ví, jakou použije analytickou techniku a zároveň si stanoví maximální akceptovanou šíři intervalu spolehlivosti. Pro ilustraci lze užít klasickou tabulku (tabulka 1), která určuje šíři intervalů spolehlivosti pro proporci u jedné proměnné (např. procento příznivců určité strany, nakupujících určitý výrobek).
[1] Síla statistického testu je pravděpodobnost, že zamítnu nulovou hypotézu, pokud tato hypotéza v populaci neplatí. Jinými slovy jde o pravděpodobnost správného zamítnutí nulové hypotézy. Logicky požadujeme, aby tato hodnota byla co nejvyšší, tedy aby test detekoval rozdíly či souvislosti, pokud možno s co nejvyšší jistotou.
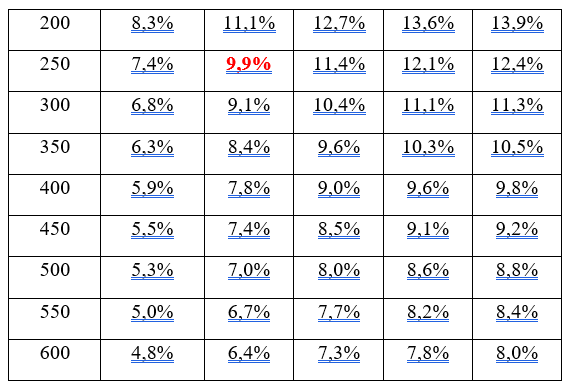
Pokud například očekávám, že výrobek bude nakupovat 20 % spotřebitelů (v tabulce hledám v prvním řádku hodnotu 0,2) a interval spolehlivosti chci mít široký maximálně 10 %, snadno v tabulce nahlédnu, že velikost výzkumného souboru pro takovou přesnost bude 250 jednotek (zvýrazněná hodnota v tabulce).
Cohen, J. 1988. Statistical Power Analysis for the Behavioral Sciences (2nd Edition). Routledge.
Chcete-li se dozvědět více o postupech vedoucích k určení velikosti výzkumných souborů, přihlaste se na kurz, Stanovení velikosti výzkumného souboru, kde vás seznámíme s postupy pro vybírání výzkumných jednotek a s postupy sloužící k určení velikosti výběru.






Velmi potřebný článek. Velmi aktuální problematika, protože ekonomické časopisy jsou zaplaveny statistickými analýzami, které nacházejí korelace apod., ale neodhalují skutečný vztah příčin a důsledků. Zejména je to problém zkoumání malých souborů respondentů (např. lokálních jevů), nedostatku informací (např. u malých firem) nebo jedinečných událostí v podnikání, kupř. originálních inovací (tedy inovátor se inovací odklání výrazně od průměru, který dosahují méně kreativní podnikatelé). Články v časopisech pak se často věnují těmto „průměrným“ a nepostihují „progresívní“ firmy a trendy (v zárodečných podobách).
Díky za příznivou reakci. Ano, problém mnoha empirických studií je, že byly získány na malých souborech a díky náhodě tak vyšel zajímavý výsledek. Ostatně zejména v psychologii řeší tzv. replikační krizi, kdy mnoho dosud slavných studií při pokusu o replikaci nebylo potvrzeno. Seriózní výzkumník, který chce užívat kvantitativní techniky pro zpracování svých výzkumných dat se musí již před navržením detailního designu otázkou velikosti výzkumného souboru zabývat. Ostatně sílí tendence toto žádat již v grantových přihláškách, při registraci výzkumných projektů apod. Jde o součást širšího hnutí označovaného jako open science.
Dobrý den, děkuji za přínosný článek psaný jasně a srozumitelně. Ráda bych se zeptala jak je tomu u studií exploračního typu. V případě, že je znám celkový počet souboru, ze kterého je vybrán soubor výzkumný, je nějaké doporučení k jeho velikosti? Děkuji
Přeji pěkný den.
Obecně platí, že na velikosti populace nezávisí, pokud není výběr velkou částí populace. U exploračních studií žádný jednoduchý výpočet velikosti výběru (pokud vím) není, protože zde se nelze opřít o nic typu síly testu či požadované šíře intervalu spolehlivosti. I zde ale jistě platí, že větší soubory jsou potřebné, když pracuji s více proměnnými najednou a když mám větší variabilitu dat.
Díky za otázku,
Petr Soukup