Falešná korelace

Jak spolu souvisí smrt a sýr…
V tomto článku si povíme o něčem, co je známo pod pojmem falešná či nepravá korelace (anglicky spurious correlation). Korelační koeficient udává míru asociace mezi dvěma číselnými proměnnými. Jedná se o číslo z intervalu <-1, 1>. Pokud se korelace rovná mínus jedné nebo jedné, můžeme hovořit o lineární závislosti. V těchto případech leží všechny námi uvažované body na společné přímce. Nesmíme ovšem zapomenout, že korelační koeficient udává pouze míru lineárního vztahu. Pokud se v datech vyskytuje jiný druh závislosti, korelačním koeficientem jej nezachytíme. Vysoké hodnoty korelačního koeficientu mohou mít několik příčin. První z nich může být skutečnost, že sledované veličiny jsou opravdu korelované. Příkladem takovýchto veličin mohou být otáčky vrtule větrné elektrárny a množství vyrobené elektrické energie. Dalším příkladem mohou být výška člověka a velikost nohy. U takovýchto veličin nepochybujeme o správnosti vysoké hodnoty korelace. Jinou příčinnou vysokého korelačního koeficientu může být odlehlé pozorování. Jedná se o nebezpečný jev obzvláště v případě, kdy máme k dispozici málo pozorování. Tento problém se dá vyřešit například odstraněním odlehlých hodnot z datového souboru. Problematičtější může být následující případ. Vysokou hodnotu korelace můžeme nalézt také mezi veličinami, jako jsou výše platu a velikost nohou. Při hlubším zamyšlení můžeme objevit veličinu, která ovlivňuje obě výše zmíněné. Touto „skrytou“ veličinou je pohlaví. Pro muže obecně platí, že mají větší velikost bot než ženy. Také platí, že muži mají vyšší příjmy než ženy, a to i na stejných pozicích. Vliv původně neuvažovaného pohlaví nám tedy může způsobit vysokou hodnotu korelačního koeficientu. Falešná korelace nám ale může vzniknou mezi dvěma naprosto odlišnými číselnými řadami, u kterých nejsme schopni společnou vysvětlující příčinu nalézt.
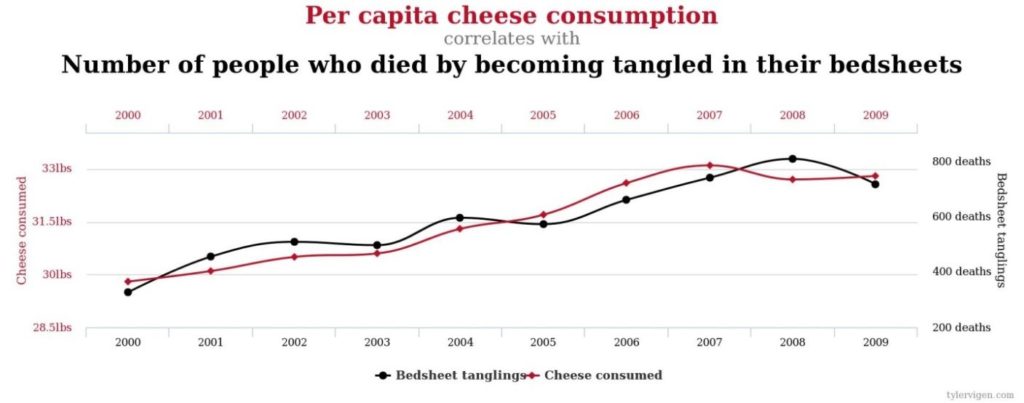
Obr. 1 Spotřeba sýru na osobu a počet lidí, kteří zemřeli v důsledku zamotání se do prostěradel
Jedná se o korelaci mezi spotřebou sýru na osobu v librách a počtem nezaviněných úmrtí způsobené zamotáním se do prostěradel. Jelikož je korelační koeficient bezrozměrná veličina, nevadí nám rozdílné jednotky. Výsledný korelační koeficient je roven r = 0,947, což je velmi vysoká hodnota. Pokud bychom usuzovali pouze z hodnoty korelačního koeficientu, řekli bychom, že tyto dvě veličiny spolu dozajista velice úzce souvisí. Korelační koeficient nicméně neimplikuje kauzalitu. Asi nemůžeme obecně říci, že s rostoucí spotřebou sýru na osobu poroste počet takto zemřelých lidí. Máme zde dvě rostoucí řady, které spolu nesouvisí.
Dalším příklad je zobrazen na následujícím obrázku.
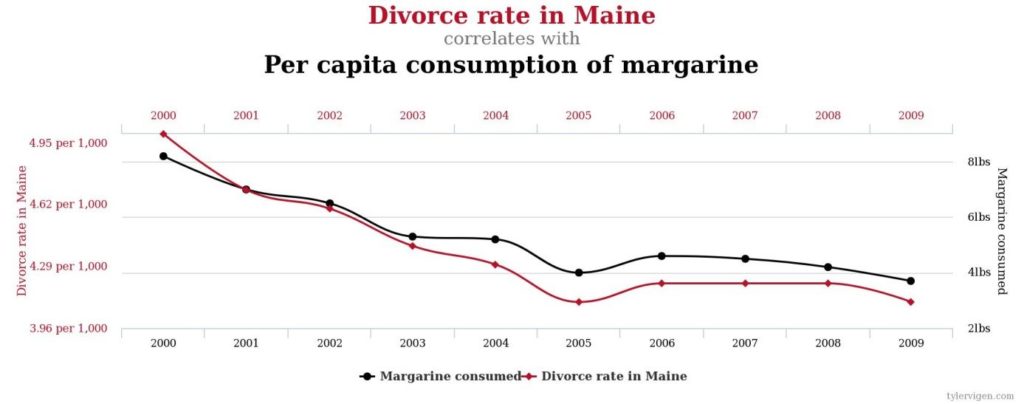
Obr. 2 Rozvodovost v Maine a spotřeba margarínu na osobu
V tomto případě se jedná o dvě klesající řady. Jedna z nich nám udává počet rozvodů na 1000 obyvatel ve státě Maine, druhá zobrazuje spotřebu margarínu na osobu v librách. Hodnota korelačního koeficientu je r = 0,993. Tato hodnota se velmi blíží 1, což indikuje téměř přímou úměrnost. Nicméně ani zde se nedá hovořit o jakékoliv kauzalitě. Nemůžeme obecně říci, že s klesající spotřebou margarínu také klesne rozvodovost ve státě Maine.
Použité grafy jsou ze stránky http://www.tylervigen.com/spurious-correlations, kde je možnost podívat na spoustu dalších příkladů falešných korelací.
Na příkladu počtu úmrtí a sýru, popřípadě rozvodovosti a spotřeby margarínu je vidět, jak spolu mohou korelovat zcela odlišné číselné řady. Musíme si také uvědomit, že v pozadí sledovaných veličin hraje významnou roli čas. V případě časových řad musíme být velice opatrní, pokud chceme o korelacích hovořit. O spoustě dalších vlastnostech, typů, výhod a nevýhod korelačních koeficientů se můžete dozvědět například na našem kurzu korelační analýzy.
Rádi byste se o statistice a analýze dat dozvěděli více? Chcete se stát mistrem ve svém oboru nebo si jen potřebujete doplnit znalosti? V ACREA nabízíme širokou nabídku kurzů pro váš profesní růst. Máte-li jiný dotaz. Nebojte se využít naši nezávaznou konzultaci, při které vám rádi zodpovíme všechny vaše dotazy a najdeme vhodné řešení.





